题目内容
【题目】如图,已知 A、B是线段MN上的两点,MN4,MA1,MB1.以A为中心顺 时针旋转点M,以B为中心逆时针旋转点N,使MN 两点重合成一点C,构成△ABC,设ABx.(1)则x的取值范围是_________;(2)△ABC的最大面积是_________.
C 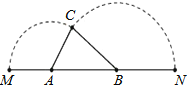
【答案】![]()
![]()
【解析】
(1)因为所求AB或x在△ABC中,所以可利用三角形三边之间的关系即两边之和大于第三边,两边之差小于第三边进行解答.
(2)在△ABC中,AB的值固定不变,即可视为底边不变,但是因为三角形形状不固定,
高在发生变化,所以造成面积不固定,需分情况进行讨论.具体分①若点D在线段AB上,②若点D在线段MA上两种情况.
(1)∵在△ABC中,AC=1,AB=x,BC=3x.
∴![]() ,
,
解得1<x<2;
(2)在△ABC中,作CD⊥AB于D,
设CD=h,△ABC的面积为S,则S=![]() xh,
xh,
①若点D在线段AB上,
则![]() +
+![]() =x,
=x,
∴(3x)2h2=x22x![]() +1h2,
+1h2,
即x![]() =3x4,
=3x4,
∴x2(1h2)=9x224x+16,
即x2h2=8x2+24x16.
∴S2=![]() x2h2=2x2+6x4=2(x
x2h2=2x2+6x4=2(x![]() )2+
)2+![]() (
(![]() ≤x<2),
≤x<2),
当x=![]() 时(满足
时(满足![]() ≤x <2)S2取最大值
≤x <2)S2取最大值![]() ,从而S取最大值
,从而S取最大值![]() ;
;
②若点D在线段MA上,
则![]()
![]() =x,
=x,
同理可,得
S2=![]() x2h2=2x2+6x4
x2h2=2x2+6x4
=2(x![]() )2+
)2+![]() (1<x≤
(1<x≤![]() ),
),
易知此时S<![]() ,
,
综合①②得,△ABC的最大面积为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目