Question

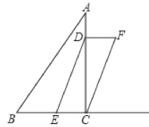
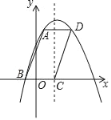
【题目】如图，ABCD与抛物线y＝﹣x2+bx+c相交于点A，B，D，点C在抛物线的对称轴上，已知点B（﹣1，0），BC＝4．

（1）求抛物线的解析式；

（2）求BD的函数表达式．

Answer 1

【答案】（1）y＝﹣x2+6x+7；（2）y＝2x+2．

【解析】

（1）由B的坐标及BC的长，求出C的坐标，确定出抛物线对称轴，利用待定系数法求出解析式即可；（2）由四边形ABCD为平行四边形可知对边平行且相等，得到AD的长，利用对称性求出D横坐标，代入抛物线解析式求出纵坐标，确定出D坐标，设出直线BD解析式为y＝kx+b，把B与D坐标代入确定出k与b的值即可．

（1）∵B（﹣1，0），BC＝4，

∴C（3，0），即抛物线对称轴为直线x＝3，

∴，

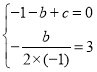解得：，

则抛物线解析式为y＝﹣x2+6x+7；

（2）∵四边形ABCD为平行四边形，

∴AD∥BC，且AD＝BC＝4，

∵A与D关于对称轴直线x＝3对称，且AD＝4，

∴A横坐标为1，D横坐标为5，

把x＝5代入抛物线解析式得：y＝12，即D（5，12），

设直线BD解析式为y＝kx+b，

把B与D坐标代入得：，

解得： ，

则直线BD的解析式为y＝2x+2．