题目内容
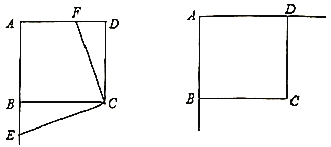
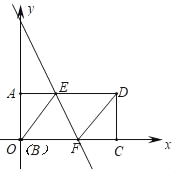
【题目】如图,矩形ABCD中,AD=8,AB=4,将此矩形折叠,使点B与点D重合,折痕为EF,连接BE、DF,以B为原点建立平面直角坐标系,使BC、BA边分别在x轴和y轴的正半轴上.

(1)试判断四边形BFDE的形状,并说明理由;
(2)求直线EF的解析式.
【答案】(1)四边形BFDE是菱形,见解析;(2)y=﹣2x+10.
【解析】
(1)根据矩形的性质及等腰三角形的特点即可求出四边 相等,故可求解;
(2)设AE=x,得BE=DE=8﹣x,利用在Rt△ABE中利用勾股定理求出x,得到E点和点F的坐标,再根据待定系数法确定函数关系式进行求解.
解:(1)四边形BFDE是菱形,理由如下:
由题意可知:DE=BE,DF=BF,∠DEF=∠BEF,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEF=∠BFE,
∴∠BEF=∠BFE,
∴BE=BF,
∴BE=BF=DF=DE,
∴四边形BFDE是菱形;
(2)设AE=x,
∵AD=8,AB=4,
∴BE=DE=8﹣x,
在Rt△ABE中,∠BAE=90°,
∴AB2+AE2=BE2,
∴42+x2=(8﹣x)2,
解得:x=3,
∴AE=3,BF=5,
∴E点的坐标是(3,4),点F的坐标是(5,0),
设直线EF的解析式为y=kx+b,
可得方程组![]() ,
,
解这个方程组得![]() ,
,
∴直线EF的解析式是y=﹣2x+10.

【题目】我国男性的体质系数计算公式是:m=![]() ×100%,其中W表示体重(单位:kg),H表示身高(单位:cm).通过计算出的体质系数m对体质进行评价.具体评价如下表:
×100%,其中W表示体重(单位:kg),H表示身高(单位:cm).通过计算出的体质系数m对体质进行评价.具体评价如下表:
m | <80% | 80%~90% | 90%~110% | 110%~120% | >120% |
评价结果 | 明显消瘦 | 消瘦 | 正常 | 过重 | 肥胖 |
(1)某男生的身高是170cm,体重是75kg,他的体质评价结果是 ;
(2)现从某校九年级学生中随机抽取n名男生进行体质评价,评价结果统计如下:
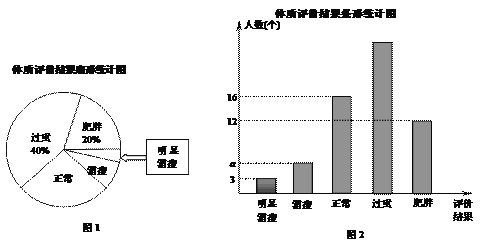
①抽查的学生数n= ;图2中a的值为 ;
②图1中,体质评价结果为“正常”的所在扇形圆心角为 °;
(3)若该校九年级共有男生480人,试估计该校九年级体质评价结果为“过重”或“肥胖”的男生人数.
【题目】某校为了了解学生对语文、数学、英语、物理四科的喜爱程度(每人只选一科),特对八年级某班进行了调查,并绘制成如下频数和频率统计表和扇形统计图:
科目 | 频数 | 频率 |
语文 |
| 0.5 |
数学 | 12 |
|
英语 | 6 |
|
物理 |
| 0.2 |

(1)求出这次调查的总人数;
(2)求出表中![]() 的值;
的值;
(3)若该校八年级有学生1000人,请你算出喜爱英语的人数,并发表你的看法.