��Ŀ����
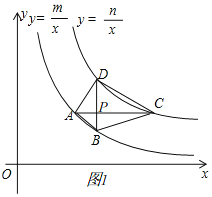
����Ŀ����ͼ���ı���ABCD���ĸ�����ֱ��ڷ���������y=![]() ��y=
��y=![]() ��x��0��0��m��n����ͼ���ϣ��Խ���BD��y�ᣬ��BD��AC�ڵ�P����֪��B�ĺ�����Ϊ4��
��x��0��0��m��n����ͼ���ϣ��Խ���BD��y�ᣬ��BD��AC�ڵ�P����֪��B�ĺ�����Ϊ4��
��1����m=4��n=20ʱ��
������P��������Ϊ2����ֱ��AB�ĺ�������ʽ��
������P��BD���е㣬���ж��ı���ABCD����״����˵�����ɣ�
��2���ı���ABCD�ܷ��Ϊ�����Σ����ܣ����ʱm��n֮���������ϵ�������ܣ���˵�����ɣ�

���𰸡���1����ֱ��AB�Ľ���ʽΪy=��![]() x+3�����ɼ����������ı���ABCD�����Σ���2���ı���ABCD���������Σ����ɼ�����.
x+3�����ɼ����������ı���ABCD�����Σ���2���ı���ABCD���������Σ����ɼ�����.
����������1������ȷ������A��B���꣬�����ô���ϵ�������ɵó����ۣ�
����ȷ������D���꣬����ȷ������P���꣬�������PA��PC�����ɵó����ۣ�
��2����ȷ����B��4��![]() ���������ó�A��4-t��
���������ó�A��4-t��![]() +t����������4-t����
+t����������4-t����![]() +t��=m�����ɵó���D��4��8-
+t��=m�����ɵó���D��4��8-![]() �������ɵó����ۣ�
�������ɵó����ۣ�
��1������ͼ1��
��m=4��
�෴��������Ϊy=![]() ����x=4ʱ��y=1��
����x=4ʱ��y=1��
��B��4��1����
��y=2ʱ��
��2=![]() ��
��
��x=2��
��A��2��2����
��ֱ��AB�Ľ���ʽΪy=kx+b��
��![]() ��
��
��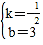 ��
��
��ֱ��AB�Ľ���ʽΪy=-![]() x+3��
x+3��
���ı���ABCD�����Σ�
�������£���ͼ2��
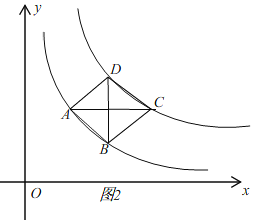
�ɢ�֪��B��4��1����
��BD��y�ᣬ
��D��4��5����
�ߵ�P���߶�BD���е㣬
��P��4��3����
��y=3ʱ����y=![]() �ã�x=
�ã�x=![]() ��
��
��y=![]() �ã�x=
�ã�x=![]() ��
��
��PA=4-![]() =
=![]() ��PC=
��PC=![]() -4=
-4=![]() ��
��
��PA=PC��
��PB=PD��
���ı���ABCDΪƽ���ı��Σ�
��BD��AC��
���ı���ABCD�����Σ�
��2���ı���ABCD���������Σ�
���ɣ����ı���ABCD�������Σ�
��PA=PB=PC=PD������Ϊt��t��0����
��x=4ʱ��y=![]() =
=![]() ��
��
��B��4��![]() ����
����
��A��4-t��![]() +t����
+t����
����4-t����![]() +t��=m��
+t��=m��
��t=4-![]() ��
��
���D��������Ϊ![]() +2t=
+2t=![]() +2��4-
+2��4-![]() ��=8-
��=8-![]() ��
��
��D��4��8-![]() ����
����
��4��8-![]() ��=n��
��=n��
��m+n=32��




