题目内容
【题目】对于抛物线y=x2﹣4x+3.
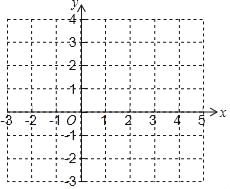
(1)它与x轴交点的坐标为 ,与y轴交点的坐标为 ,顶点坐标为 .
(2)在坐标系中利用描点法画出此抛物线;
x | … |
|
|
|
|
| … |
y | … |
|
|
|
|
| … |
【答案】(1) (1,0)和(3,0),(0,3),(2,﹣1);(2)0,1,2,3,4,3,0,﹣1,0,3.
【解析】
(1)利用待定系数法配方法即可解决问题;
(2)利用描点法即可解决问题.
(1)对于抛物线y=x2﹣4x+3令x=0得到y=3,令y=0得到x2﹣4x+3=0,解得x=1或3,∴与x轴交点的坐标为(1,0)和(3,0),与y轴交点的坐标为(0,3);
∵y=x2﹣4x+3=(x﹣2)2﹣1,∴顶点坐标(2,﹣1).
故答案为:(1,0)和(3,0),(0,3),(2,﹣1);
(2)取点(0,3),(1,0),(2,﹣1),(3,0),(4,3),利用描点法画出图象如图所示:
故答案为:0,1,2,3,4,3,0,﹣1,0,3.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目