题目内容
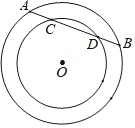
【题目】如图,在△ABC中,∠B=46°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=_____.

【答案】67°.
【解析】
先根据三角形内角和定理计算出∠BAC+∠BCA=180°﹣∠B=134°,则利用邻补角定义计算出∠DAC+∠FCA=180°﹣∠BAC+180°﹣∠BCA=226°,再根据角平分线定义得到∠EAC=![]() ∠DAC,∠ECA=
∠DAC,∠ECA=![]() ∠FCA,所以∠EAC+∠ECA=
∠FCA,所以∠EAC+∠ECA=![]() (∠DAC+∠FCA)=113°,然后再利用三角形内角和计算∠AEC的度数.
(∠DAC+∠FCA)=113°,然后再利用三角形内角和计算∠AEC的度数.
解:∵∠B=46°,
∴∠BAC+∠BCA=180°﹣46°=134°,
∴∠DAC+∠FCA=180°﹣∠BAC+180°﹣∠BCA=360°﹣134°=226°,
∵AE和CE分别平分∠DAC和∠FCA,
∴∠EAC=![]() ∠DAC,∠ECA=
∠DAC,∠ECA=![]() ∠FCA,
∠FCA,
∴∠EAC+∠ECA=![]() (∠DAC+∠FCA)=113°,
(∠DAC+∠FCA)=113°,
∴∠AEC=180°﹣(∠EAC+∠ECA)=180°﹣113°=67°.
故答案为:67°.

 阅读快车系列答案
阅读快车系列答案【题目】现有A、B两种手机上网计费方式,收费标准如下表所示:
计费方式 | 月使用费/元 | 包月上网时间/分 | 超时费/(元/分) |
A | 30 | 120 | 0.20 |
B | 60 | 320 | 0.25 |
设上网时间为x分钟,
(1)若按方式A和方式B的收费金额相等,求x的值;
(2)若上网时间x超过320分钟,选择哪一种方式更省钱?
【题目】某校举办了一![]() 次趣味数学竞赛,满分
次趣味数学竞赛,满分![]() 分,学生得分均为整数,成绩达到
分,学生得分均为整数,成绩达到![]() 分及以上为合格,达到
分及以上为合格,达到![]() 分及以上为优秀这次竞赛中,甲、乙两组学生成绩如下(单位:分).
分及以上为优秀这次竞赛中,甲、乙两组学生成绩如下(单位:分).
甲组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
乙组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 68分 | a | 376 | 90% | 30% |
乙组 | b | c | 196 | 80% | 20% |
以上成绩统计分析表中![]() ________分,
________分,![]() _________分,
_________分,![]() ________分;
________分;
(2)小亮同学说:![]() 这次竞赛我得了
这次竞赛我得了![]() 分,在我们小组中排名属中游略偏上!
分,在我们小组中排名属中游略偏上!![]() 观察上面表格判断,小亮可能是甲、乙哪个组的学生?并说明理由.
观察上面表格判断,小亮可能是甲、乙哪个组的学生?并说明理由.
(3)如果你是该校数学竞赛的教练员,现在需要你选择一组同学代表学校参加复赛,你会选择哪一组?并说明理由.