题目内容
某工厂投入生产一种机器的总成本为2000万元.当该机器生产数量至少为10台,但不超过70台时,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如下表:
| x(单位:台) | 10 | 20 | 30 |
| y(单位:万元∕台) | 60 | 55 | 50 |
(2)求该机器的生产数量;
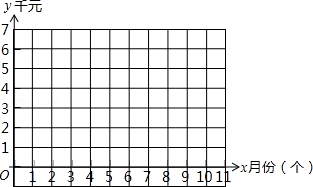
(3)市场调查发现,这种机器每月销售量z(台)与售价a(万元∕台)之间满足如图所示的函数关系.该厂生产这种机器后第一个月按同一售价共卖出这种机器25台,请你求出该厂第一个月销售这种机器的利润.(注:利润=售价﹣成本)

解:(1)设y与x之间的关系式为y=kx+b,由题意,得 ,解得:
,解得: 。
。
∴y=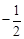 x+65。
x+65。
∵该机器生产数量至少为10台,但不超过70台,∴10≤x≤70。
(2)由题意,得xy=2000,即 ,即
,即 。
。
解得:x1=50,x2=80>70(舍去)。
答:该机器的生产数量为50台。
(3)设每月销售量z(台)与售价a(万元∕台)之间的函数关系式为 ,由函数图象,得
,由函数图象,得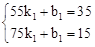 ,解得:
,解得: 。
。
∴z=﹣a+90。
当z=25时,a=65;当x=50时,y=40,
∴总利润为:25(65﹣40)=625(万元).。
答:该厂第一个月销售这种机器的利润为625万元
解析试题分析:(1)设y与x之间的关系式为y=kx+b,运用待定系数法就可以求出其关系式,由该机器生产数量至少为10台,但不超过70台就可以确定自变量的取值范围。
(2)根据每台的成本乘以生产数量等于总成本建立方程求出其解即可。
(3)设每月销售量z(台)与售价a(万元∕台)之间的函数关系式为z=ka+b,运用待定系数法求出其解析式,再将z=25代入解析式求出a的值,就可以求出每台的利润,从而求出总利润。

某地区为了进一步缓解交通拥堵问题,决定修建一条长为6千米的公路.如果平均每天的修建费y(万元)与修建天数x(天)之间在30≤x≤120,具有一次函数的关系,如下表所示.
| x | 50 | 60 | 90 | 120 |
| y | 40 | 38 | 32 | 26 |
(2)后来在修建的过程中计划发生改变,政府决定多修2千米,因此在没有增减建设力量的情况下,修完这条路比计划晚了15天,求原计划每天的修建费.
增强公民的节约意识,合理利用天然气资源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
| 每月用气量 | 单价(元/m3) |
| 不超出75m3的部分 | 2.5 |
| 超出75m3不超出125m3的部分 | a |
| 超出125m3的部分 | a+0.25 |
(2)若调价后每月支出的燃气费为y(元),每月的用气量为x(m3),y与x之间的关系如图所示,求a的值及y与x之间的函数关系式;
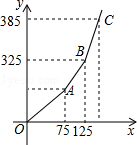
(3)在(2)的条件下,若乙用户2、3月份共用1气175m3(3月份用气量低于2月份用气量),共缴费455元,乙用户2、3月份的用气量各是多少?
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,则下列四个结论错误的是( )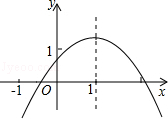
| A.c>0 | B.2a+b=0 | C.b2﹣4ac>0 | D.a﹣b+c>0 |
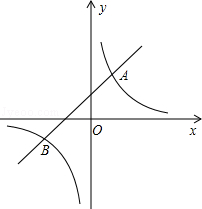
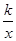 的图象相交于点A(-2,a),并且与x轴相交于点B。
的图象相交于点A(-2,a),并且与x轴相交于点B。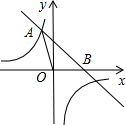
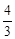 x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B'处.
x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B'处.
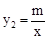 的图象交于A(2,4)、B(﹣4,n)两点.
的图象交于A(2,4)、B(﹣4,n)两点.