题目内容
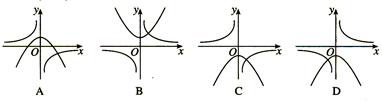
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,则下列四个结论错误的是( )
| A.c>0 | B.2a+b=0 | C.b2﹣4ac>0 | D.a﹣b+c>0 |
D
解析试题分析:A、因为二次函数的图象与y轴的交点在y轴的上方,所以c>0,正确;
B、由已知抛物线对称轴是直线x=1=﹣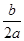 ,得2a+b=0,正确;
,得2a+b=0,正确;
C、由图知二次函数图象与x轴有两个交点,故有b2﹣4ac>0,正确;
D、直线x=﹣1与抛物线交于x轴的下方,即当x=﹣1时,y<0,即y=ax2+bx+c=a﹣b+c<0,错误.
故选D.
考点:二次函数的图象与系数的关系

练习册系列答案
相关题目
某工厂投入生产一种机器的总成本为2000万元.当该机器生产数量至少为10台,但不超过70台时,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如下表:
| x(单位:台) | 10 | 20 | 30 |
| y(单位:万元∕台) | 60 | 55 | 50 |
(2)求该机器的生产数量;
(3)市场调查发现,这种机器每月销售量z(台)与售价a(万元∕台)之间满足如图所示的函数关系.该厂生产这种机器后第一个月按同一售价共卖出这种机器25台,请你求出该厂第一个月销售这种机器的利润.(注:利润=售价﹣成本)

已知二次函数y=ax2+bx+c的图象如图,①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1),其中结论正确的有( )
| A.③④ | B.③⑤ | C.③④⑤ | D.②③④⑤ |
抛物线y=(x﹣1)2﹣3的对称轴是( )
| A.y轴 | B.直线x=﹣1 | C.直线x=1 | D.直线x=﹣3 |
如图,二次函数y=ax2+bx+c的图象经过(-1,0)、(0,3),下列结论中错误的是( )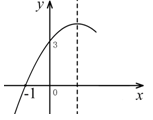
| A.abc<0 | B.9a+3b+c=0 | C.a-b="-3" | D. 4ac﹣b2<0 |
如图,抛物线y=ax2+bx+c与x轴交于点(1,0),对称轴为x=1,则下列结论中正确的是( )
A. |
B.当 时,y随x的增大而增大 时,y随x的增大而增大 |
C. |
D. 是一元二次方程 是一元二次方程 的一个根 的一个根 |
 ,第8天时,雨雪停止附近的胜利农场前来支援,合作6天,完成了兴化农场所有的收割任务.图1是机械收割的亩数y1(亩)和人工收割的亩数y2(亩)与时间x(天)之间的函数图象.图2是剩余的农作物的亩数w(亩)与时间x天之间的函数图象,请结合图象回答下列问题.
,第8天时,雨雪停止附近的胜利农场前来支援,合作6天,完成了兴化农场所有的收割任务.图1是机械收割的亩数y1(亩)和人工收割的亩数y2(亩)与时间x(天)之间的函数图象.图2是剩余的农作物的亩数w(亩)与时间x天之间的函数图象,请结合图象回答下列问题.
 与
与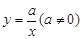 在同一直角坐标系中的图象可能是( )
在同一直角坐标系中的图象可能是( )