题目内容
如图,直线y=- x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B'处.
x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B'处.
求(1)点B'的坐标.(2)直线AM所对应的函数关系式
(1)(-4,0);(2)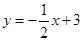 .
.
解析试题分析:(1)分别令y=0,x=0求出直线y=- x+8与x轴、y轴交点A、B的坐标.根据折叠性质可得
x+8与x轴、y轴交点A、B的坐标.根据折叠性质可得 进而求得点B'的坐标(2)设OM=m则B'M=BM=8-m
进而求得点B'的坐标(2)设OM=m则B'M=BM=8-m
根据勾股定理得;m2+42=(8-m)2,求出m=3,所以,M(0,3)设直线AM的解析式为y=kx+b,图象过(6,0)(0,3)代入可求得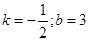 所以求出直线AM所对应的函数关系式.
所以求出直线AM所对应的函数关系式.
试题解析:(1)A(6,0),B(0,8)
OA=6,OB="8" 根据勾股定理得:AB=10
根据折叠性质可得
 A B'=AB=10,
A B'=AB=10, O B'=10-6=4
O B'=10-6=4 B'(-4,0)
B'(-4,0)
(2)设OM=m则B'M=BM=8-m
根据勾股定理得;
m2+42=(8-m)2 m=3
m=3 M(0,3)
M(0,3)
设直线AM的解析式为y=kx+b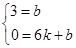
解得: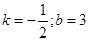
 直线AM所对应的函数关系式
直线AM所对应的函数关系式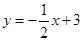
考点:1.折叠问题;2.一次函数的解析式;3.一次函数图象与坐标轴交点.

练习册系列答案
相关题目
某工厂投入生产一种机器的总成本为2000万元.当该机器生产数量至少为10台,但不超过70台时,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如下表:
| x(单位:台) | 10 | 20 | 30 |
| y(单位:万元∕台) | 60 | 55 | 50 |
(2)求该机器的生产数量;
(3)市场调查发现,这种机器每月销售量z(台)与售价a(万元∕台)之间满足如图所示的函数关系.该厂生产这种机器后第一个月按同一售价共卖出这种机器25台,请你求出该厂第一个月销售这种机器的利润.(注:利润=售价﹣成本)


 2m)x+m+1,求当m为何值时.
2m)x+m+1,求当m为何值时.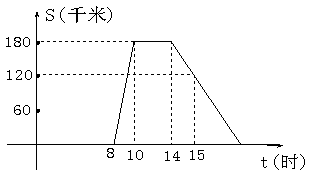
 、
、 分别在
分别在 轴、
轴、 轴的正半轴上,且
轴的正半轴上,且 ,点
,点 为线段
为线段 的中点.
的中点. 的长度为________________;
的长度为________________;
 ,当点
,当点 在第一象限时,求直线
在第一象限时,求直线 所对应的函数的解析式;
所对应的函数的解析式;
 、
、 分别在
分别在 轴的负半轴上,且
轴的负半轴上,且 ,以
,以 为边在第三象限内作正方形
为边在第三象限内作正方形 ,请求出线段
,请求出线段 长度的最大值,并直接写出此时直线
长度的最大值,并直接写出此时直线

 ,第8天时,雨雪停止附近的胜利农场前来支援,合作6天,完成了兴化农场所有的收割任务.图1是机械收割的亩数y1(亩)和人工收割的亩数y2(亩)与时间x(天)之间的函数图象.图2是剩余的农作物的亩数w(亩)与时间x天之间的函数图象,请结合图象回答下列问题.
,第8天时,雨雪停止附近的胜利农场前来支援,合作6天,完成了兴化农场所有的收割任务.图1是机械收割的亩数y1(亩)和人工收割的亩数y2(亩)与时间x(天)之间的函数图象.图2是剩余的农作物的亩数w(亩)与时间x天之间的函数图象,请结合图象回答下列问题.