Question

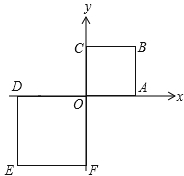
【题目】在研究相似问题时，甲、乙同学的观点如下： 甲：将边长为3、4、5的三角形按图1的方式向外扩张，得到新三角形，它们的对应边间距为1，则新三角形与原三角形相似．
乙：将邻边为3和5的矩形按图2的方式向外扩张，得到新的矩形，它们的对应边间距均为1，则新矩形与原矩形不相似．
对于两人的观点，下列说法正确的是（　　）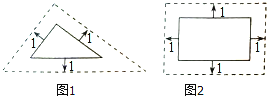

A.两人都对
B.两人都不对
C.甲对，乙不对
D.甲不对，乙对

Answer 1

【答案】A
【解析】解答：甲：根据题意得：AB∥ ，AC∥ ，BC∥ ， ∴∠A=∠ ，∠B=∠ ，
∴△ABC∽△ ，
∴甲说法正确；
乙：∵根据题意得：AB=CD=3，AD=BC=5，则 = =3+2=5， = =5+2=7，
∴ ， ，
∴ ，
∴新矩形与原矩形不相似．
∴乙说法正确．
故选：A．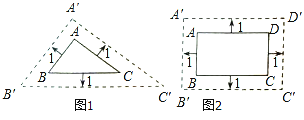

分析：甲：根据题意得：AB∥ ，AC∥ ，BC∥ ，可证得∠A=∠ ，∠B=∠ ，由两角对应相等两三角形相似得△ABC∽△ ；乙：根据题意得：AB=CD=3，AD=BC=5，则 =C′D′=3+2=5，A′D′= =5+2=7，则可得 ，即新矩形与原矩形不相似．此题考查了相似三角形以及相似多边形的判定．
【考点精析】解答此题的关键在于理解相似图形的相关知识，掌握形状相同，大小不一定相同（放大或缩小）;判定:①平行；②两角相等；③两边对应成比例，夹角相等；④三边对应成比例，以及对相似三角形的判定的理解，了解相似三角形的判定方法:两角对应相等，两三角形相似（ASA）；直角三角形被斜边上的高分成的两个直角三角形和原三角形相似； 两边对应成比例且夹角相等，两三角形相似（SAS）；三边对应成比例，两三角形相似（SSS）．