Question

【题目】已知：如图，△ABC∽△ADE ， AE：EC=5：3，BC=6cm，∠A=40°，∠C=45°．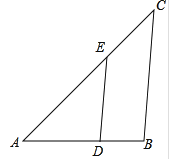

（1）求∠ADE的大小；
（2）求DE的长．

Answer 1

【答案】
（1）

解答：在△ABC中，∠A=40°，∠C=45°，

∴∠ABC=180°-40°-45°=95°；

又∵△ABC∽△ADE，

∴∠ADE=∠ABC（相似三角形的对应角相等），

∴∠ADE =95°；

（2）

解答：∵AE：EC=5：3，

∴AE：AC=5：8；

又∵△ABC∽△ADE，BC=6cm，

∴ ，即

∴DE= cm．

【解析】先由三角形的内角和是180°求得∠ABC=95°；再由相似三角形的对应角相等得出∠ADE=∠ABC ， 最后由等量代换求得∠ADE的大小；由AE：EC=5：3求得AE：AC=5：8，再根据相似三角形的对应边成比例求得DE的长度．此题主要考查了相似三角形的性质：相似三角形的对应角相等，对应边成比例．
【考点精析】认真审题，首先需要了解相似三角形的性质(对应角相等，对应边成比例的两个三角形叫做相似三角形)．