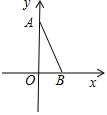题目内容
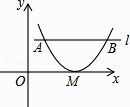
【题目】已知抛物线y=x2﹣2x﹣3与x轴交于A,B两点,点A在点B的左侧.
(1)求A,B两点的坐标和此抛物线的对称轴;
(2)设此抛物线的顶点为C,点D与点C关于x轴对称,求四边形ACBD的面积.
【答案】
(1)解:令y=0,则x2﹣2x﹣3=0,
解得:x1=﹣1,x2=3.
∵点A在点B的左侧.
∴点A的坐标是(﹣1,0),B的坐标是(3,0).
∵y=﹣﹣x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线对称轴是x=1
(2)解:∵顶点C的坐标是(1,﹣4),D与点C关于x轴对称,
∴D的坐标是(1,4).
∴AB=3﹣(﹣1)=4,CD=4﹣(﹣4)=8,
∴四边形ACBD的面积是: ![]() ABCD=
ABCD= ![]() ×4×8=16.
×4×8=16.
【解析】(1)令y=0解方程即可求得A和B的横坐标,然后利用配方法即可求得对称轴和顶点坐标;(2)首先求得D的坐标,然后利用面积公式即可求解.

【题目】为满足同学们课外阅读的需求,某中学图书馆向出版社邮购科普系列图书,每本书单价为16元,书的价钱和邮费是通过邮局汇款,相关的书价折扣、邮费和汇款的汇费如下表所示(总费用=总书价+总邮费+总汇费)
购书数量 | 折扣 | 邮费 | 汇费 |
不超过10本 | 九折 | 6元 | 每100元汇款需汇费1元 (汇款不足100元时按100元汇款收汇费) |
超过10本 | 八折 | 总书价的10% | 每100元汇款需汇费1元 (汇款不足100元的部分不收汇费) |
(1)若一次邮购7本,共需总费用为 元.
(2)已知学校图书馆需购图书的总数是10的整倍数,且超过10本.
①若分次邮购,分别汇款,每次邮购10本,总费用为1064元时,共邮购了多本图书?
②若你是学校图书馆负责人,从节约的角度出发,在“每次邮购10本“与“一次性邮购”这两种方式中选择一种,你会选择哪一种?计算并说明理由.
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数m | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的频率= | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计:当n很大时,摸到白球的频率将会接近多少?(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(白球)是多少?
(3)试估算盒子里黑、白两种颜色的球各有多少只?