题目内容
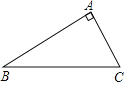
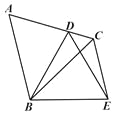
【题目】如图,△ABC是等边三角形,点D为 AC边上一点,以BD为边作等边△BDE, 连接CE.若CD=1,CE=3,则BC=_____.
【答案】4
【解析】试题分析:在CB上取一点G使得CG=CD,即可判定△CDG是等边三角形,可得CD=DG=CG,易证∠BDG=∠EDC,即可证明△BDG≌△EDC,可得BG=CE,即可解题.
解:在CB上取一点G使得CG=CD,
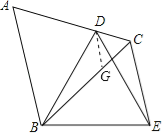
∵△ABC是等边三角形,∴∠ACB=60°,
∴△CDG是等边三角形,
∴CD=DG=CG,
∵∠BDG+∠EDG=60°,∠EDC+∠EDG=60°,
∴∠BDG=∠EDC,
在△BDG和△EDC中,
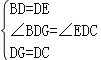 ,
,
∴△BDG≌△EDC(SAS),
∴BG=CE,
∴BC=BG+CG=CE+CD=4,
故答案为:4.

练习册系列答案
相关题目
【题目】某检修小组从A地出发,在东西方向的公路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶,纪录如下(单位:km)
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 |
﹣4 | +7 | ﹣9 | +8 | +6 | ﹣5 | ﹣2 |
则收工时距A地多远?在第几次纪录时距A地最远?
A. 2千米 第1次 B. 1千米 第2次
C. 2千米 第4次 D. 1千米 第5次