题目内容
【题目】已知正方形ABCD的对角线AC,BD相交于点O.
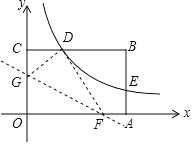
(1)如图1,E,G分别是OB,OC上的点,CE与DG的延长线相交于点F.若DF⊥CE,求证:OE=OG;
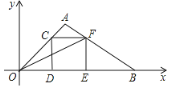
(2)如图2,H是BC上的点,过点H作EH⊥BC,交线段OB于点E,连结DH交CE于点F,交OC于点G.若OE=OG,
①求证:∠ODG=∠OCE;
②当AB=1时,求HC的长.

【答案】(1)证明见解析;(2)①证明见解析;②![]()
【解析】试题分析:(1)欲证明OE=OG,只要证明△DOG≌△COE(ASA)即可;
(2)①欲证明∠ODG=∠OCE,只要证明△ODG≌△OCE即可;
②设CH=x,由△CHE∽△DCH,可得![]() ,即HC2=EHCD,由此构建方程即可解决问题;
,即HC2=EHCD,由此构建方程即可解决问题;
试题解析:(1)证明:如图1中,∵四边形ABCD是正方形,∴AC⊥BD,OD=OC,∴∠DOG=∠COE=90°,∴∠OEC+∠OCE=90°,∵DF⊥CE,∴∠OEC+∠ODG=90°,∴∠ODG=∠OCE,∴△DOG≌△COE(ASA),∴OE=OG.
(2)①证明:如图2中,∵OG=OE,∠DOG=∠COE=90°OD=OC,∴△ODG≌△OCE,∴∠ODG=∠OCE.
②解:设CH=x,∵四边形ABCD是正方形,AB=1,∴BH=1﹣x,∠DBC=∠BDC=∠ACB=45°,∵EH⊥BC,∴∠BEH=∠EBH=45°,∴EH=BH=1﹣x,∵∠ODG=∠OCE,∴∠BDC﹣∠ODG=∠ACB﹣∠OCE,∴∠HDC=∠ECH,∵EH⊥BC,∴∠EHC=∠HCD=90°,∴△CHE∽△DCH,∴![]() ,∴HC2=EHCD,∴x2=(1﹣x)1,解得x=
,∴HC2=EHCD,∴x2=(1﹣x)1,解得x=![]() 或
或![]() (舍弃),∴HC=
(舍弃),∴HC=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目