Question

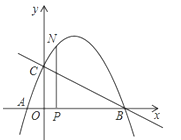
【题目】如图，点A 坐标为（1，1），点C是线段OA上的一个动点（不运动至O，A两点）过点C作CD⊥x轴，垂足为D，以CD为边在右侧作正方形CDEF，连接AF并延长交x轴的正半轴于点B，连接OF，若以B、E、F为顶点的三角形与△OEF相似，，则B的坐标是 ___________

Answer 1

【答案】（，0）或（3，0）

【解析】

根据点A坐标是（1，1）可以确定∠AOB=45°，又四边形CDEF是正方形，所以0D=CD=DE，即可证明△OFE的边OE=2EF，再根据“以B，E，F为顶点的三角形与△OFE相似”分①EF=2EB，②EB=2EF两种情况讨论，根据△ACF与△AOB相似，相似三角形对应高的比等于对应边的比列出比例式计算即可求出正方形的边长，从而OB的长亦可求出．

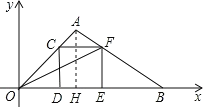
过点A作AH⊥OB，

∵点A的坐标为(1,1)，

∴AH=OH=1,∠AOB=45°，

∴OD=CD，

设CF=x，

∵四边形CDEF是正方形，

∴CF∥DE，CD=CF=EF=DE，

∴CD=CF=EF=DE=x，

∴OE=OD+DE=2EF，

∵以B，E，F为顶点的三角形与△OFE相似，

∴①EF=2EB,则EB=x，

∴OB=OE+EB=2x+x=x，

∵CF∥DE，

∴△ACF∽△AOB，

∴=，

即=1x，

解得x=，

OB=×=，

∴点B的坐标为(,0)，

②EB=2EF时，则EB=2x，

∴OB=OE+EB=2x+2x=4x，

∵CF∥DE，

∴△ACF∽△AOB，

∴=，

即=1x，

解得x=，

OB=4x=4×=3，

∴点B的坐标为(3,0).

综上所述,点B的坐标是(,0)或(3,0).

故答案为：(,0)或(3,0).