题目内容
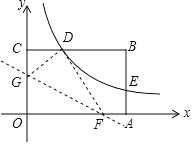
【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为BC边上的点,AB=BD,反比例函数![]() 在第一象限内的图象经过点D(m,2)和AB边上的点E(n,
在第一象限内的图象经过点D(m,2)和AB边上的点E(n,![]() ).
).
(1)求m、n的值和反比例函数的表达式.
(2)将矩形OABC的一角折叠,使点O与点D重合,折痕分别与x轴,y轴正半轴交于点F,G,求线段FG的长.
【答案】(1)y=![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据题意得出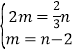 ,解方程即可求得m、n的值,然后根据待定系数法即可求得反比例函数的解析式;
,解方程即可求得m、n的值,然后根据待定系数法即可求得反比例函数的解析式;
(2)设OG=x,则GD=OG=x,CG=2﹣x,根据勾股定理得出关于x的方程,解方程即可求得DG的长,过F点作FH⊥CB于H,易证得△GCD∽△DHF,根据相似三角形的性质求得FG,最后根据勾股定理即可求得.
(1)∵D(m,2),E(n,![]() ),
),
∴AB=BD=2,
∴m=n﹣2,
∴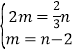 ,解得
,解得![]() ,
,
∴D(1,2),
∴k=2,
∴反比例函数的表达式为y=![]() ;
;
(2)设OG=x,则GD=OG=x,CG=2﹣x,
在Rt△CDG中,x2=(2﹣x)2+12,
解得x=![]() ,
,
过F点作FH⊥CB于H,
∵∠GDF=90°,
∴∠CDG+∠FDH=90°,
∵∠CDG+∠CGD=90°,
∴∠CGD=∠FDH,
∵∠GCD=∠FHD=90°,
∴△GCD∽△DHF,
∴![]() ,即
,即![]() ,
,
∴FD=![]() ,
,
∴FG=![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了从甲、乙两名选手中选拔出一个人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表.
甲、乙射击成绩统计表
平均数(环) | 中位数(环) | 方差 | 命中10环的次数 |
甲 | 7 | 0 | |
乙 | 1 |
甲、乙射击成绩折线统计图

(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?
【题目】中秋节期间某水库养殖场为适应市场需求,连续用![]() 天时间,采用每天降低水位以减少捕捞成本的办法.对水库中某种鲜鱼进行捕捞销售,第
天时间,采用每天降低水位以减少捕捞成本的办法.对水库中某种鲜鱼进行捕捞销售,第![]() 天(
天(![]() 且
且![]() 为整数)的捕捞与销售的相关信息如下:
为整数)的捕捞与销售的相关信息如下:
鲜鱼销售单价(元 |
|
单位捕捞成本(元 |
|
捕捞量 |
|
假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出.
(1)求第![]() 天的收入
天的收入![]() (元)与
(元)与![]() (天)之间的函数关系式?(当天收入
(天)之间的函数关系式?(当天收入![]() 日销售额-日捕捞成本)
日销售额-日捕捞成本)
(2)在第几天![]() 取得最大值,最大值是多少?
取得最大值,最大值是多少?