Question

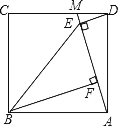
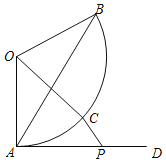
【题目】如图，在扇形AOB中，OA＝OB＝4，∠AOB＝120°，点C是弧AB上的一个动点（不与点A，B重合），射线AD与扇形AOB所在⊙O相切，点P在射线AD上，连接AB，OC，CP，若AP＝2，则CP的取值范围是_____．

Answer 1

【答案】

【解析】

根据切线的性质得到∠OAD＝90°，由OA＝OB，得到∠OAB＝30°，就可求出∠BAP，进而求出∠APB＝90°，求出PB长．当O、C、P三点在一条直线上时，求出CP的长，则CP的取值范围可求出．

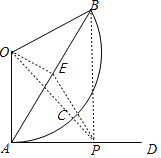
解：如图，当O、C、P三点在一条直线上时，

∵射线AD与扇形AOB所在⊙O相切，

∴∠OAP＝90°，

∵AO＝4，AP＝ ，

∴，

∴PC＝，

过点O作OE⊥AB于点E，连接PE、PB，

∵OA＝OB＝4，∠AOB＝120°，

∴∠OAB＝∠OBA＝30°，

∴AE＝BE＝2，∠BAP＝60°，

∴AE＝AP，

∴△AEP是等边三角形，

∴∠AEP＝60°，

∴∠EPB＝30°，

∴∠APB＝90°，

∴，

∵点C不与A、B重合，

∴PC的取值范围是．

故答案为：．