题目内容
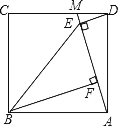
【题目】如图，点M是正方形ABCD边CD上一点，连接AM，作DE⊥AM于点E，BF⊥AM于点F，连接BE，若AF＝1，四边形ABED的面积为6，则∠EBF的余弦值是（ ）
A.
B.
C.
D.
【答案】B
【解析】
首先证明△ABF≌△DEA得到BF=AE；设AE=x，则BF=x，DE=AF=1，利用四边形ABED的面积等于△ABE的面积与△ADE的面积之和得到
xx+x×1=6，解方程求出x得到AE=BF=3，则EF=x-1=2，然后利用勾股定理计算出BE，最后利用余弦的定义求解．
∵四边形ABCD为正方形，
∴BA＝AD，∠BAD＝90°，
∵DE⊥AM于点E，BF⊥AM于点F，
∴∠AFB＝90°，∠DEA＝90°，
∵∠ABF+∠BAF＝90°，∠EAD+∠BAF＝90°，
∴∠ABF＝∠EAD，
在△ABF和△DEA中
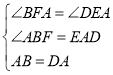
∴△ABF≌△DEA（AAS），
∴BF＝AE；
设AE＝x，则BF＝x，DE＝AF＝1，
∵四边形ABED的面积为6，
∴
，解得x1＝3，x2＝﹣4（舍去），
∴EF＝x﹣1＝2，
在Rt△BEF中，
，
∴
．
故选B．
挑战100单元检测试卷系列答案
【题目】体育老师为了解本校九年级女生1分钟“仰卧起坐”体育测试项目的达标情况，从该校九年级136名女生中，随机抽取了20名女生，进行了1分钟仰卧起坐测试，获得数据如下：
收集数据：抽取20名女生的1分钟仰卧起坐测试成绩(个)如下：
38 46 42 52 55 43 59 46 25 38
35 45 51 48 57 49 47 53 58 49
（1）整理、描述数据：请你按如下分组整理、描述样本数据，把下列表格补充完整：
范围 |
|
|
|
|
|
|
|
人数 |
(说明：每分钟仰卧起坐个数达到49个及以上时在中考体育测试中可以得到满分)
（2）分析数据：样本数据的平均数、中位数、满分率如下表所示：
平均数 | 中位数 | 满分率 |
46.8 | 47.5 |
|
得出结论：①估计该校九年级女生在中考体育测试中1分钟“仰卧起坐”项目可以得到满分的人数；
②该中心所在区县的九年级女生的1分钟“仰卧起坐”总体测试成绩如下：
平均数 | 中位数 | 满分率 |
45.3 | 49 |
|
请你结合该校样本测试成绩和该区县总体测试成绩，为该校九年级女生的1分钟“仰卧起坐”达标情况做一下评估．
