题目内容
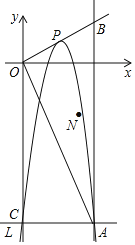
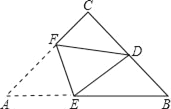
【题目】如图,在矩形AOBC中,O为坐标原点,OA、OB分别在x轴、y轴上,点B的坐标为(0,3),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为____________.

【答案】(![]() ,
,![]() )
)
【解析】
过点D作DE⊥y轴于E,根据矩形的性质可得∠CBO=∠BOA=90°,OB=3,AO=BC,然后根据锐角三角函数即可求出AO和BC,再根据折叠的性质可得BD=BC=![]() ,∠ABD=∠CBA=60°,然后利用锐角三角函数求出BE和ED,即可求出OE,从而求出点D的坐标.
,∠ABD=∠CBA=60°,然后利用锐角三角函数求出BE和ED,即可求出OE,从而求出点D的坐标.
解:过点D作DE⊥y轴于E

∵四边形AOBC是矩形,点B的坐标为(0,3),∠ABO=30°,
∴∠CBO=∠BOA=90°,OB=3,AO=BC
∴∠CBA=∠CBO-∠ABO=60°,
在Rt△BAO中,AO=OB·tan∠ABO=![]()
∴BC=![]()
根据折叠的性质可知BD=BC=![]() ,∠ABD=∠CBA=60°
,∠ABD=∠CBA=60°
∴∠EBD=∠ABD-∠ABO=30°
在Rt△EBD中,DE=BD·sin∠EBD=![]() ,BE=BD·cos∠EBD=
,BE=BD·cos∠EBD=![]()
∴OE=OB-BE=![]()
∴点D的坐标为(![]() ,
,![]() )
)
故答案为:(![]() ,
,![]() ).
).

练习册系列答案
相关题目