��Ŀ����
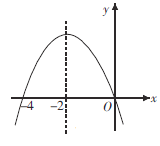
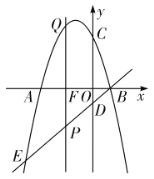
����Ŀ����ͼ�����κ���y=![]() x2+bx+c��ͼ�����B��0��1����C��4��3�����㣬��x�ύ�ڵ�D����E������B�͵�C��ֱ����x�ύ�ڵ�A��
x2+bx+c��ͼ�����B��0��1����C��4��3�����㣬��x�ύ�ڵ�D����E������B�͵�C��ֱ����x�ύ�ڵ�A��
(1)����κ����Ľ���ʽ��
(2)��x������һ����P�����ŵ�P���ƶ������ڵ�Pʹ��PBC��ֱ�������Σ����������P�����ꣻ
(3)������P��A���������x������x����������ÿ��2����λ���ٶ��˶���ͬʱ����QҲ��A���������ÿ��a����λ���ٶ�������AC�˶����Ƿ������A��P��QΪ���������������ABD���ƣ������ڣ�ֱ��д��a��ֵ���������ڣ�˵�����ɣ�

���𰸡�(1)�����߽���ʽy=![]() x2�C
x2�C![]() x+1��(2)��P������1��0������3��0������
x+1��(2)��P������1��0������3��0������![]() ��0������
��0������![]() ��0����(3)a=
��0����(3)a=![]() ��
��![]() ��
��
��������
(1) ��B��C�������������κ�������ʽ,ͨ����������������b��c��ֵ�����������������ʽ;
(2)��P��x��0�����ɡ�PBC��ֱ�������Σ��֡�CBP=90�����BPC=90������������ۣ����ù��ɶ����ɵ�x��ֵ�������õ�P������;
(3)��������С�APQ�ס�ADB���APQ�ס�ABD,���Ӧ�߳ɱ����������a��ֵ.
(1)�߶��κ���y=0.5x2+bx+c��ͼ�����B��0��1����C��4��3�����㣬
��![]() �����
�����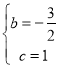 ��
��
�������߽���ʽy=![]() x2�C
x2�C![]() x+1��
x+1��
(2)���P������x��0����
�ߵ�P��x��0������B��0��1������C��4��3����
��PB=![]() =
=![]() ��
��
CP=![]() =
=![]() ��
��
BC=![]() =2
=2![]() ��
��
����BCP=90������BP2=BC2+CP2��
��x2+1=20+x2�C8x+25����x=![]() ��
��
����CBP=90������CP2=BC2+BP2��
��x2+1+20=x2�C8x+25����x=![]() ��
��
����BPC=90������BC2=BP2+CP2��
��x2+1+x2�C8x+25=20��
��x1=1��x2=3��
������������P������1��0������3��0������![]() ��0������
��0������![]() ��0����
��0����
(3)a=![]() ��
��![]() ��
��
�������߽���ʽy=![]() x2�C
x2�C![]() x+1��x�ύ�ڵ�D����E��
x+1��x�ύ�ڵ�D����E��
��0=![]() x2�C
x2�C![]() x+1����x1=1��x2=2�����D��1��0����
x+1����x1=1��x2=2�����D��1��0����
�ߵ�B��0��1����C��4��3����
��ֱ��BC����ʽy=![]() x+1��
x+1��
��y=0ʱ��x=�C2�����A���C2��0����
�ߵ�A���C2��0������B��0��1������D��1��0����
��AD=3��AB=![]() ��
��
�辭��t�룬��AP=2t��AQ=at��
����APQ�ס�ADB��
��![]() ����
����![]() ����a=
����a=![]() ��
��
����APQ�ס�ABD����![]() ����
����![]() ����a=
����a=![]() ��
��
����������a=![]() ��
��![]() ��
��

����Ŀ���ڡ���������ڡ�����֮�ʣ�ijУ�ٰ����ԡ��ҵ��ഺ��������Ϊ������ݽ������� ���Ӳμӱ�����ѧ���������ȡ����ѧ�����ݽ��ɼ�����ͳ��(�ȼ���A�����㣬B�����ã�C��һ�㣬D���ϲ�)��������������ͳ��ͼ��(������Ϣδ����)��
�ȼ� | ���� |
A | m |
B | 20 |
C | n |
D | 10 |

�����ͳ��ͼ���е���Ϣ����������⣺
(1)��ι���ȡ��________���μ��ݽ�������ѧ����ͳ��ͼ��a��________��b��________��
(2)����Уѧ������2000�ˣ�������μ����ݽ�������������Ƴɼ��ﵽ������ж����ˣ�
(3)���ݽ������ɼ�ΪA�ȼ���ѧ����ǡ����2��Ů���������ѧ��Ϊ��������A�ȼ���ѧ���г�ȡ����ͬѧ�μ�ȫ���ݽ������������һ��������һ��Ů���ĸ��ʣ�