题目内容
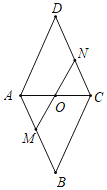
【题目】如图，在菱形ABCD中MN分别在AB、CD上且AM=CN，MN与AC交于点O，连接BO若∠DAC=62°，则∠OBC的度数为（ ）
A. 28°B. 52°C. 62°D. 72°
【答案】A
【解析】
连接OB，根据菱形的性质以及AM=CN，利用ASA可得△AMO≌△CNO，可得AO=CO，然后可得BO⊥AC，继而可求得∠OBC的度数．
解：连接OB，
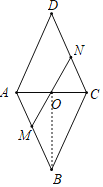
∵四边形ABCD为菱形
∴AB∥CD，AB=BC，
∴∠MAO=∠NCO，∠AMO=∠CNO，
在△AMO和△CNO中，
∵
，
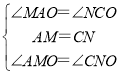∴△AMO≌△CNO（ASA），
∴AO=CO，
∵AB=BC，
∴BO⊥AC，
∴∠BOC=90°，
∵∠DAC=62°，
∴∠BCA=∠DAC=62°，
∴∠OBC=90°-62°=28°．
故选：A．
练习册系列答案
阅读快车系列答案
相关题目
