题目内容
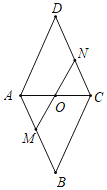
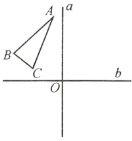
【题目】如图所示，已知
和互相垂直的两条直线
、
，垂足为点
.
与关于直线成轴对称，
与关于直线成对称.那么下列说法正确的是（ ）
A.可以由平移得到B.可以由翻折得到
C.与成轴对称D.与成中心对称
【答案】D
【解析】
根据题意在图形中画出
和
，然后根据平移、翻转、轴对称、中心对称的定义逐个判断选项正确与否.
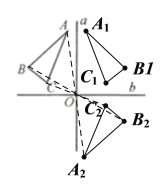
首先根据题意画出和，如图所示，然后分析每个选项：
A.平移是指在平面内，将一个图形上的所有点都按照某个方向作相同距离的移动，这样的图形运动叫做图形的平移，故此项不正确，
B.翻折是将一个图形沿着某一条直线翻折过来，直线两旁的部分能够相互重合，故此项不正确，
C.如果一个图形沿着一条直线对折,两侧的图形能够完全重合,称这两个图形关于这条直线对称，也称这两个图形成轴对称，故此项不正确，
D.把一个图形绕着某一个点旋转
，如果它能够与另一个图形重合,则这两个图形关于这个点中心对称，故此项正确，
故答案为D.
练习册系列答案
相关题目
