题目内容
【题目】用棋子摆成的“上”字型图案如图所示现察此图案的规律,并回答:
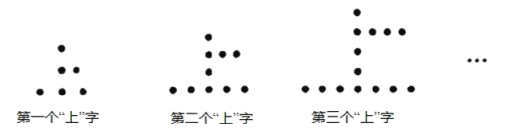
(1)依照此规律,第五个图形中共有 个棋子,第八个图形中共有 个棋子.
(2)第![]() (
(![]() 为正整数)个图形中共有 个棋子.
为正整数)个图形中共有 个棋子.
(3)根据(2)中的结论,第几个图形中有2022个棋子?
【答案】(1)22,34;(2)![]() ;(3)第505个图形中有2022个棋子
;(3)第505个图形中有2022个棋子
【解析】
(1)根据图形可以写出前几个图形中棋子的个数,从而发现棋子的变化规律,从而可以得到第五个和第八个图形中的棋子个数;
(2)根据(1)中发现的规律,可以得到第n(n为正整数)个图形中棋子的个数;
(3)根据(2)中的结果,可以求得第几个图形中有2022个棋子.
(1)由图可得:
第一图形中的“上”字中棋子的个数为:3×2=6,
第二图形中的“上”字中棋子的个数为:5×2=10,
第三图形中的“上”字中棋子的个数为:7×2=14,
…,
则第五个图形中共有:(2×5+1)×2=22(个),
第八个图形中共有:(2×8+1)×2=34(个).
故答案为:22,34;
(2)第n(n为正整数)个图形中共有:(2n+1)×2=(4n+2)(个).
故答案为:(4n+2);
(3)令4n+2=2022,
解得:n=505,
即第505个图形中有2022个棋子.

练习册系列答案
相关题目