题目内容
【题目】在△ABC中,∠ACB=90°,经过点C的⊙O与斜边AB相切于点P.
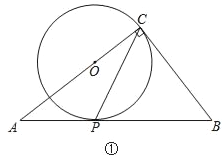
(1)如图①,当点O在AC上时,试说明2∠ACP=∠B;
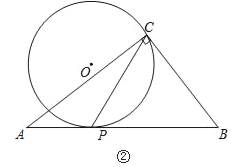
(2)如图②,AC=8,BC=6,当点O在△ABC外部时,求CP长的取值范围.
【答案】(1)2∠ACP=∠B;(2)当点O在△ABC外时,![]() <CP≤8.
<CP≤8.
【解析】分析:(1)根据BC与AC垂直得到BC与圆相切,再由AB与![]() 相切于点P,利用切线长定理得到
相切于点P,利用切线长定理得到![]() ,利用等边对等角得到一对角相等,再由
,利用等边对等角得到一对角相等,再由![]() 等量代换即可得证;
等量代换即可得证;
(2)在![]() 中,利用勾股定理求出AB的长,根据AC与BC垂直,得到BC与
中,利用勾股定理求出AB的长,根据AC与BC垂直,得到BC与![]() 相切,连接连接OP、AO,再由AB与
相切,连接连接OP、AO,再由AB与![]() 相切,得到OP垂直于AB,设OC=x,则OP=x,OB=BCOC=6x,求出PA的长,利用勾股定理列出关于x的方程,求出方程的解得到x的值,确定出BO的长,根据AC=AP,OC=OP,得到AO垂直平分CP,根据面积法求出CP的长,由题意可知,当点P与点A重合时,CP最长,即可确定出CP的范围.
相切,得到OP垂直于AB,设OC=x,则OP=x,OB=BCOC=6x,求出PA的长,利用勾股定理列出关于x的方程,求出方程的解得到x的值,确定出BO的长,根据AC=AP,OC=OP,得到AO垂直平分CP,根据面积法求出CP的长,由题意可知,当点P与点A重合时,CP最长,即可确定出CP的范围.
详解:(1)当点O在AC上时,OC为![]() 的半径,
的半径,
∵BC⊥OC,且点C在![]() 上,
上,
∴BC与![]() 相切,
相切,
∵![]() 与AB边相切于点P,
与AB边相切于点P,
∴BC=BP,
∴![]()
∵![]()
∴![]()
即2∠ACP=∠B;
(2)在△ABC中, ![]()
如图,当点O在CB上时,OC为![]() 的半径,
的半径,
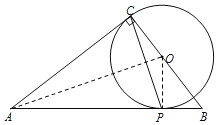
∵AC⊥OC,且点C在![]() 上,
上,
∴AC与![]() 相切,
相切,
连接OP、AO,
∵![]() 与AB边相切于点P,
与AB边相切于点P,
∴OP⊥AB,
设OC=x,则OP=x,OB=BCOC=6x,
∵AC=AP,
∴BP=ABAP=108=2,
在△OPA中,![]()
根据勾股定理得:![]() ,即
,即![]()
解得:![]()
在△ACO中,![]()
∴![]()
∵AC=AP,OC=OP,
∴AO垂直平分CP,
∴根据面积法得:![]() 则符合条件的CP长大于
则符合条件的CP长大于![]()
由题意可知,当点P与点A重合时,CP最长,
综上,当点O在△ABC外时,![]()

练习册系列答案
相关题目