题目内容
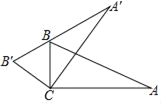
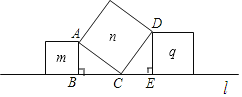
【题目】如图，在直线l上有三个正方形m、q、n，若m、q的面积分别为5和11，则n的面积（ ）
A.4B.6C.16D.55
【答案】C
【解析】
运用正方形边长相等，再根据同角的余角相等可得∠BAC=∠DCE，然后证明△ACB≌△DCE，再结合全等三角形的性质和勾股定理来求解即可．
解：由于m、q、n都是正方形，所以AC=CD，∠ACD=90°；
∵∠ACB+∠DCE=∠ACB+∠BAC=90°，
∴∠BAC=∠DCE，且AC=CD，∠ABC=∠DEC=90°
∴△ACB≌△DCE（AAS），
∴AB=CE，BC=DE；
在Rt△ABC中，由勾股定理得：AC2=AB2+BC2=AB2+DE2，
即Sn=Sm+Sq=11+5=16，
∴正方形n的面积为16，
故选C．
练习册系列答案
阅读快车系列答案
相关题目
【题目】2019年4月25日至27日，第二届“一带一路”国际合作高峰论坛在北京举行，本届论坛期间，中国同30多个国家签署经贸合作协议。我国准备将
地的茶叶1000吨和
地的茶叶500吨销往“一带一路”沿线的
地和
地，地和地对茶叶需求分别为900吨和600吨，已知从、两地运茶叶到、两地的运费（元/吨）如下表所示，设地运到地的茶叶为
吨，
|
| |
| 35 | 40 |
| 30 | 45 |
（1）用含的代数式填空：
地运往地的茶叶吨数为___________，地运往地的茶叶吨数为___________，地运往地的茶叶吨数为___________.
（2）用含（吨）的代数式表示总运费
（元），并直接写出自变量的取值范围；
（3）求最低总运费，并说明总运费最低时的运送方案.
