题目内容
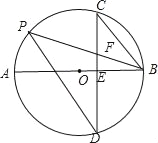
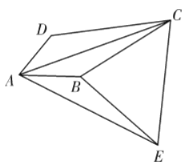
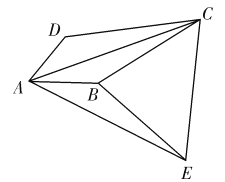
【题目】如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() 得
得![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:![]() ≌
≌![]() ;
;
(2)求证:![]() ;
;
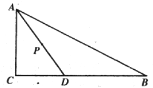
(3)若![]() ,点
,点![]() 在四边形
在四边形![]() 内部运动,且满足
内部运动,且满足![]() ,求点
,求点![]() 运动路径的长度.
运动路径的长度.
【答案】(1)详见解析;(2)详见解析;(3)![]() .
.
【解析】
(1)根据等式的基本性质可得![]() ,然后利用SAS即可证出
,然后利用SAS即可证出![]() ≌
≌![]() ;
;
(2)根据四边形的内角和和全等三角形的性质可得![]() ,从而求出∠CBE=90°,根据勾股定理可得
,从而求出∠CBE=90°,根据勾股定理可得![]() ,根据等边三角形的判定及性质可得
,根据等边三角形的判定及性质可得![]() ,从而证出结论;
,从而证出结论;
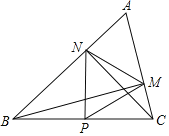
(3)如图,设![]() 为满足条件的点,将
为满足条件的点,将![]() 绕着点
绕着点![]() 顺时针旋转60度得
顺时针旋转60度得![]() ,连接
,连接![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() , DB,先利用SAS证出
, DB,先利用SAS证出![]() ≌
≌![]() ,从而得出
,从而得出![]() ,∠AQD=∠AFB,然后证出
,∠AQD=∠AFB,然后证出![]() 为等边三角形,△ADB为等边三角形,从而得出
为等边三角形,△ADB为等边三角形,从而得出![]() , DB=AB=2,然后根据勾股定理的逆定理可得
, DB=AB=2,然后根据勾股定理的逆定理可得![]() ,根据四点共圆证出点
,根据四点共圆证出点![]() 的路径为过
的路径为过![]() 、
、![]() 、
、![]() 三点的圆上
三点的圆上![]() ,求出圆心角和半径即可求出点
,求出圆心角和半径即可求出点![]() 运动路径的长度.
运动路径的长度.
证明:(1)∵![]()
∴![]()
∴![]()
在![]() 和
和![]() 中
中
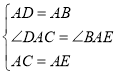
∴![]() ≌
≌![]()
(2)在四边形![]() 中
中
![]()
∵![]() ≌
≌![]()
∴![]() ,
,![]()
∴![]()
∴![]()
∴![]()
又∵![]() ,
,![]()
∴△AEC为等边三角形
∴![]()
∴![]()
(3)如图,设![]() 为满足条件的点,将
为满足条件的点,将![]() 绕着点
绕着点![]() 顺时针旋转60度得
顺时针旋转60度得![]() ,连接
,连接![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() , DB.
, DB.

∵![]()
∴![]()
∴![]()
在![]() 和
和![]() 中
中
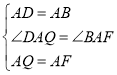
∴![]() ≌
≌![]()
∴![]() ,∠AQD=∠AFB,
,∠AQD=∠AFB,
∵![]() ,AQ=AF,∠DAB=60°,AD=AB
,AQ=AF,∠DAB=60°,AD=AB
∴![]() 为等边三角形,△ADB为等边三角形
为等边三角形,△ADB为等边三角形
∴![]() , DB=AB=2
, DB=AB=2
∵![]()
∴![]()
∴![]()
∴![]()
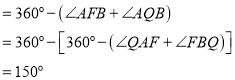
∵∠BCD=30°
∴∠DQB+∠BCD=180°
∴点![]() 的路径为过
的路径为过![]() 、
、![]() 、
、![]() 三点的圆上
三点的圆上![]()
设圆心为![]() ,连接OD、OB
,连接OD、OB
则![]() ,
,
∴△OBD为等边三角形
∴![]() ,
,
∴点![]() 的运动的路径长为:
的运动的路径长为:![]() .
.

【题目】一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:
会员年卡类型 | 办卡费用(元) | 每次游泳收费(元) |
A 类 | 50 | 25 |
B 类 | 200 | 20 |
C 类 | 400 | 15 |
例如,购买A类会员年卡,一年内游泳20次,消费50+25×20=550元,若一年内在该游泳馆游泳的次数介于40~50次之间,则最省钱的方式为( )
A.购买A类会员卡B.购买B类会员年卡
C.购买C类会员年卡D.不购买会员年卡