题目内容
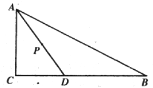
【题目】如图，在
中，
，
，点
在边
上，
，
．点
是线段
上一动点，当半径为
的
与
的一边相切时，
的长为____________．
【答案】
或
或
【解析】
根据勾股定理得到AB、AD的值，再分3种情况根据相似三角形性质来求AP的值．
解：∵在
中，
，
，
，
∴AD=
在Rt△ACB中，，，，
∴CB=6+10=16
∵AB =AC +BC
AB=
①当⊙P与BC相切时,设切点为E,连结PE, 则PE=4，∠AEP=90°
∵AD=BD=10
∴∠EAP=∠CBA, ∠C=∠AEP=90°
∴△APE∽△ACB
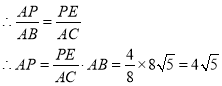
②当⊙P与AC相切时，设切点为F，连结PF,则PF=4，∠AFP=90°
∵∠C=∠AFP=90°
∠CAD=∠FAP
∴△CAD∽△FAP
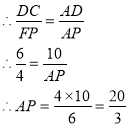
③当⊙P与BC相切时，设切点为G，连结PG,则PG=4，∠AGP=90°
∵∠C=∠PGD=90°
∠ADC=∠PDG
∴△CAD∽△GPD
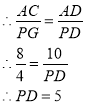
故答案为：或或5
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
