题目内容
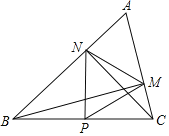
【题目】如图,在△ABC中,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM、PN、MN,则下列结论:①PM=PN;②![]() ;③若∠ABC=60°,则△PMN为等边三角形;④若∠ABC=45°,则BN=
;③若∠ABC=60°,则△PMN为等边三角形;④若∠ABC=45°,则BN=![]() PC.其中正确的是( )
PC.其中正确的是( )
A.①②③B.①②④C.①③④D.②③④
【答案】B
【解析】
根据直角三角形斜边上的中线等于斜边的一半可判断①正确;先证明△ABM∽△ACN,再根据相似三角形的对应边成比例可判断②正确;如果△PMN为等边三角形,求得∠MPN=60°,推出△CPM是等边三角形,得到△ABC是等边三角形,而△ABC不一定是等边三角形,故③错误;当∠ABC=45°时,∠BCN=45°,由P为BC边的中点,得出BN=![]() PB=
PB=![]() PC,判断④正确.
PC,判断④正确.
解:①∵BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,
∴PM=![]() BC,PN=
BC,PN=![]() BC,
BC,
∴PM=PN,正确;
②在△ABM与△ACN中,
∵∠A=∠A,∠AMB=∠ANC=90°,
∴△ABM∽△ACN,
∴![]() ,
,
∴![]() ,②正确;
,②正确;
③∵∠ABC=60°,
∴∠BPN=60°,
如果△PMN为等边三角形,
∴∠MPN=60°,
∴∠CPM=60°,
∴△CPM是等边三角形,
∴∠ACB=60°,
则△ABC是等边三角形,
而△ABC不一定是等边三角形,故③错误;
④当∠ABC=45°时,∵CN⊥AB于点N,
∴∠BNC=90°,∠BCN=45°,
∴BN=CN,
∵P为BC边的中点,
∴PN⊥BC,△BPN为等腰直角三角形
∴BN=![]() PB=
PB=![]() PC,故④正确.
PC,故④正确.
故选:B.

练习册系列答案
相关题目