题目内容
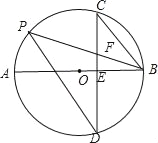
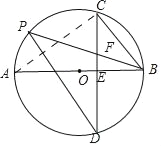
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,弦PB与CD交于点F,且FC=FB.
(1)求证:PD∥CB;
(2)若AB=26,EB=8,求CD的长度.
【答案】(1)证明见解析;(2)CD=24.
【解析】
(1)欲证明PD∥BC,只要证明∠P=∠CBF即可;
(2)由△ACE∽△CBE,可得![]() ,求出EC,再根据垂径定理即可解决问题.
,求出EC,再根据垂径定理即可解决问题.
(1)证明:∵FC=FB,
∴∠C=∠CBF,
∵∠P=∠C,
∴∠P=∠CBF,
∴PD∥BC.
(2)连接AC,
∵AB是直径,
∴∠ACB=90°,
∵AB⊥CD,
∴CE=ED,∠AEC=∠CEB=90°,
∵∠CAE+∠ACE=90°,∠ACE+∠BCE=90°,
∴∠CAE=∠BCE,
∴△ACE∽△CBE,
∴![]() ,
,
∴![]() ,
,
∴EC2=144,
∵EC>0,
∴EC=12,
∴CD=2EC=24.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目