题目内容
如图，△ABC与△DCB中，AC与BD交于点E，且∠A=∠D，AB=DC．
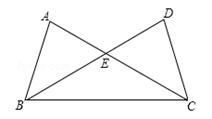
（1）求证：△ABE≌DCE；
（2）当∠AEB=50°，求∠EBC的度数。
（1）求证：△ABE≌DCE；
（2）当∠AEB=50°，求∠EBC的度数。
解（1）证明：∵在△ABE和△DCE中，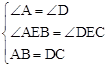
，
∴△ABE≌△DCE（AAS）。
（2）∵△ABE≌△DCE，∴BE=EC。
∴∠EBC=∠ECB。
∵∠EBC+∠ECB=∠AEB=50°，∴∠EBC=25°。
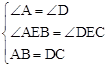，∴△ABE≌△DCE（AAS）。
（2）∵△ABE≌△DCE，∴BE=EC。
∴∠EBC=∠ECB。
∵∠EBC+∠ECB=∠AEB=50°，∴∠EBC=25°。
（1）根据AAS即可推出△ABE和△DCE全等。
（2）根据三角形全等得出EB=EC，推出∠EBC=∠ECB，根据三角形的外角性质得出∠AEB=2∠EBC，代入求出即可。
（2）根据三角形全等得出EB=EC，推出∠EBC=∠ECB，根据三角形的外角性质得出∠AEB=2∠EBC，代入求出即可。
练习册系列答案
阅读快车系列答案
相关题目
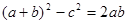，则这个三角形是（ ）
