Question

【题目】如图，∠MAN＝30°，点O为边AN上一点，以O为圆心，4为半径

作⊙O交AN于D、E两点．

⑴ 当⊙O与AM相切时，求AD的长；

⑵ 如果AD＝2，那么AM与⊙O又会有怎样的位置关系？并说明理由．

Answer 1

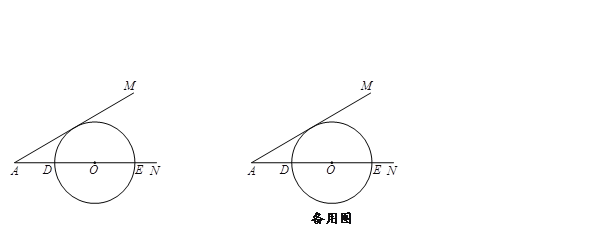
【答案】(1)4;(2) AM与⊙O相交,理由见解析

【解析】分析：(1)在Rt△AOF中，由OF求得AO，即可求解；(2)在Rt△AOF中，由AO求得OF的长，比较它与圆的半径之间的大小.

详解：⑴如图1，设切点为F，连接FO，

∵⊙O与AM相切于点F，OF为半径，

∴FO⊥AM，∴∠AFO＝90°.

∵∠A＝30°，OF＝4，

∴AO＝2OF，AD＝AO–DO＝8－4＝4．

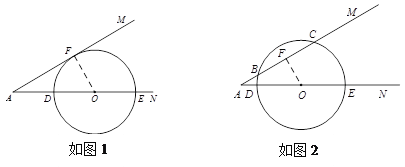
⑵AM与⊙O相交．

理由：如图2，过点O作OF⊥AM于F，

∴∠AFO＝90°，

∵AD＝2，DO＝4；∴AO＝AD＋DO＝6，又∠A＝30°，

∴OF＝AO＝×6＝3＜4，

∴AM与⊙O相交．