题目内容
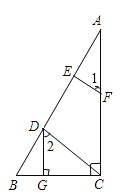
【题目】如图,已知DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB
【答案】见解析;
【解析】
灵活运用垂直的定义,注意由垂直可得90°角,由90°角可得垂直,结合平行线的判定和性质,只要证得∠ADC=90°,即可得CD⊥AB.
证明:∵ DG⊥BC,AC⊥BC(已知),
∴ ∠DGB=∠ACB=90°(垂直的定义),
∴ DG∥AC(同位角相等,两直线平行).
∴ ∠2=∠ACD(两直线平行,内错角相等).
∵ ∠1=∠2(已知),∴ ∠1=∠ACD(等量代换),
∴ EF∥CD(同位角相等,两直线平行).
∴ ∠AEF=∠ADC(两直线平行,同位角相等).
∵ EF⊥AB(已知),∴ ∠AEF=90°(垂直的定义),
∴ ∠ADC=90°(等量代换).
∴ CD⊥AB(垂直的定义).

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
【题目】某水果批发市场香蕉的价格如下表
购买香蕉数(千克) | 不超过20千克 | 20千克以上但不超过40千克 | 40千克以上 |
每千克的价格 | 6元 | 5元 | 4元 |
张强两次共购买香蕉50千克,已知第二次购买的数量多于第一次购买的数量,共付出264元,请问张强第一次,第二次分别购买香蕉多少千克?