题目内容
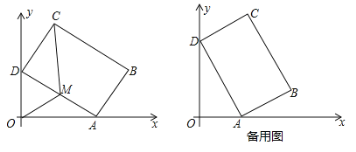
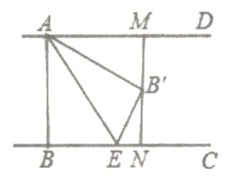
【题目】如图,已知![]() ,点
,点![]() 为射线
为射线![]() 上一个动点,连接
上一个动点,连接![]() ,将
,将![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 处,过点
处,过点![]() 作
作![]() 的垂线,分别交
的垂线,分别交![]() 于点
于点![]() 当点
当点![]() 为线段
为线段![]() 的三等分点时,
的三等分点时,![]() 的长为_____________
的长为_____________
【答案】![]() 或
或![]()
【解析】
根据平行线的性质可得MN⊥BC,MN=AB=3,∠ABE=∠MNE=∠AMN=90°,然后根据折叠的性质可得![]() =
=![]() ,
,![]() =BE,∠
=BE,∠![]() =90°,即可证出
=90°,即可证出![]() ,列出比例式,然后根据三等分点的位置分类讨论,根据勾股定理和比例式即可求出结论.
,列出比例式,然后根据三等分点的位置分类讨论,根据勾股定理和比例式即可求出结论.
解:∵![]() ,MN⊥AD
,MN⊥AD
∴MN⊥BC,MN=AB=3,∠ABE=∠MNE=∠AMN=90°
由折叠的性质可得![]() =
=![]() ,
,![]() =BE,∠
=BE,∠![]() =90°
=90°
∴![]() ,
,![]()
∴![]()
∴![]()
∴![]()
①当点![]() 为靠近点N的线段
为靠近点N的线段![]() 的三等分点时,
的三等分点时,
则![]() ,
,![]()
根据勾股定理可得AM=![]() =
=![]()
∵![]()
∴![]()
解得:![]()
∴此时BE=![]() ;
;
②当点![]() 为靠近点M的线段
为靠近点M的线段![]() 的三等分点时,
的三等分点时,
则![]() ,
,![]()
根据勾股定理可得AM=![]() =
=![]()
∵![]()
∴![]()
解得:![]()
∴此时BE=![]() ;
;
综上:BE=![]() 或
或![]()
故答案为:![]() 或
或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】车间有20名工人,某天他们生产的零件个数统计如下表.
车间20名工人某一天生产的零件个数统计表
生产零件的个数(个) | 9 | 10 | 11 | 12 | 13 | 15 | 16 | 19 | 20 |
工人人数(人) | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
(1)求这一天20名工人生产零件的平均个数;
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?