题目内容
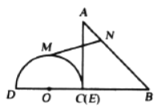
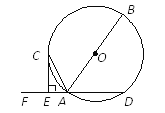
【题目】如图是小花在一次放风筝活动中某时段的示意图,她在A处时的风筝线(整个过程中风筝线近似地看作直线)与水平线构成30°角,线段AA1表示小花身高1.5米,当她从点A跑动9![]() 米到达点B处时,风筝线与水平线构成45°角,此时风筝到达点E处,风筝的水平移动距离CF=10
米到达点B处时,风筝线与水平线构成45°角,此时风筝到达点E处,风筝的水平移动距离CF=10![]() 米,这一过程中风筝线的长度保持不变,求风筝原来的高度C1D.
米,这一过程中风筝线的长度保持不变,求风筝原来的高度C1D.

【答案】风筝原来的高度为![]() 米.
米.
【解析】
设AF=x,则BF=AB+AF=9![]() +x,在Rt△BEF中求得AD=BE=
+x,在Rt△BEF中求得AD=BE=![]() ,由cos∠CAD=
,由cos∠CAD=![]() ,然后建立关于x的方程,解之求得x的值,确定AD的长,最后由CD= A Dsin∠CAD即可求出C1D.
,然后建立关于x的方程,解之求得x的值,确定AD的长,最后由CD= A Dsin∠CAD即可求出C1D.
解:设AF=x,则BF=AB+AF=9![]() +x,
+x,
在Rt△BEF中,BE=![]() ,
,
由题意知AD=BE=18+![]() x,
x,
∵CF=10![]() ,
,
∴AC=AF+CF=10![]() +x,
+x,
由cos∠CAD=![]() 可得
可得![]() ,
,
解得:x=3![]() +2
+2![]() ,
,
则AD=18+![]() (3
(3![]() +2
+2![]() )=24+2
)=24+2![]() ,
,
∴CD=ADsin∠CAD=(24+2![]() )×
)×![]() =12+
=12+![]() ,
,
则C1D=CD+C1C=12+![]() +
+![]() =
=![]() +
+![]() ;
;
答:风筝原来的高度C1D为(![]() +
+![]() )米
)米

练习册系列答案
相关题目