ћвƒњƒЏ»Ё
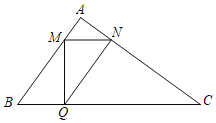
°Њћвƒњ°њ£®2018÷£÷Ёƒ£ƒв£©»зЌЉ£ђ≈„ќпѕя![]() єэµг
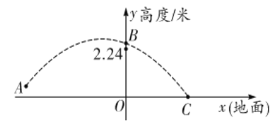
єэµг![]() £ђ”лy÷бљї”ЏµгC£Ѓ
£ђ”лy÷бљї”ЏµгC£Ѓ
£®1£©«уЄ√≈„ќпѕяµƒљвќц љ£ї
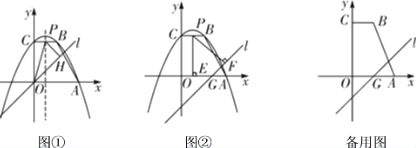
£®2£©»зЌЉҐў£ђ÷±ѕяlµƒљвќц љќ™![]() £ђ≈„ќпѕяµƒґ‘≥∆÷б”лѕяґќBCљї”ЏµгP£ђєэµгP„ч÷±ѕяlµƒієѕя£ђіє„гќ™µгH£ђЅђљ”OP£ђ«у
£ђ≈„ќпѕяµƒґ‘≥∆÷б”лѕяґќBCљї”ЏµгP£ђєэµгP„ч÷±ѕяlµƒієѕя£ђіє„гќ™µгH£ђЅђљ”OP£ђ«у![]() µƒ√жїэ£ї
µƒ√жїэ£ї
£®3£©∞—ЌЉҐў÷–µƒ÷±ѕя![]() ѕтѕ¬∆љ“∆4Єцµ•ќї≥§ґ»µ√µљ÷±ѕя
ѕтѕ¬∆љ“∆4Єцµ•ќї≥§ґ»µ√µљ÷±ѕя![]() £ђ»зЌЉҐЏ£ђ÷±ѕя
£ђ»зЌЉҐЏ£ђ÷±ѕя![]() ”лx÷бљї”ЏµгG£ЃµгP «Ћƒ±я–ќABCO±я…ѕµƒ“їµг£ђєэµгPЈ÷±р„чx÷б°Ґ÷±ѕяlµƒієѕя£ђіє„гЈ÷±рќ™µгE°ҐF£Ѓ «Јсіж‘ЏµгP£ђ єµ√“‘P°ҐE°ҐFќ™ґ•µгµƒ»эљ«–ќ «µ»—ь»эљ«–ќ£њ»фіж‘Џ£ђ÷±љ”–і≥цµгPµƒ„ш±к£ї»ф≤їіж‘Џ£ђ«лЋµ√чјн”…£Ѓ
”лx÷бљї”ЏµгG£ЃµгP «Ћƒ±я–ќABCO±я…ѕµƒ“їµг£ђєэµгPЈ÷±р„чx÷б°Ґ÷±ѕяlµƒієѕя£ђіє„гЈ÷±рќ™µгE°ҐF£Ѓ «Јсіж‘ЏµгP£ђ єµ√“‘P°ҐE°ҐFќ™ґ•µгµƒ»эљ«–ќ «µ»—ь»эљ«–ќ£њ»фіж‘Џ£ђ÷±љ”–і≥цµгPµƒ„ш±к£ї»ф≤їіж‘Џ£ђ«лЋµ√чјн”…£Ѓ
°Њір∞Є°њ£®1£©![]() £ї£®2£©
£ї£®2£©![]() £ї£®3£©іж‘Џ£ђµг
£ї£®3£©іж‘Џ£ђµг![]() „ш±кќ™(0£ђ4)їт
„ш±кќ™(0£ђ4)їт![]() їт(4£ђ6)їт
їт(4£ђ6)їт![]() £Ѓ
£Ѓ
°Њљвќц°њ
љв£Ї(1)°я≈„ќпѕя![]() єэµг
єэµг![]() £ђ
£ђ
![]() £ђ
£ђ
љвµ√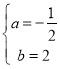 £ђ
£ђ
°а≈„ќпѕяµƒљвќц љќ™![]() £ї
£ї
(2)°яЄ√≈„ќпѕяµƒґ‘≥∆÷бќ™÷±ѕя
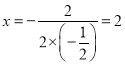 £ђ
£ђ
![]() £ђ
£ђ
»зљвЌЉҐў£ђ—”≥§![]() љї
љї![]() ÷б”Џµг
÷б”Џµг![]() £ђ°я÷±ѕя
£ђ°я÷±ѕя![]() µƒљвќц љќ™
µƒљвќц љќ™![]() £ђ
£ђ
![]() Њщќ™µ»—ь÷±љ«»эљ«–ќ£ђ
Њщќ™µ»—ь÷±љ«»эљ«–ќ£ђ
![]() £ђ
£ђ
![]() £ђ
£ђ
њ…µ√![]() £Ѓ
£Ѓ
![]() £ї
£ї
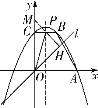
(3)іж‘Џ¬ъ„гћхЉюµƒµг![]() £ђµг
£ђµг![]() „ш±кќ™(0£ђ4)їт
„ш±кќ™(0£ђ4)їт![]() їт(4£ђ6)їт
їт(4£ђ6)їт![]() ±£ђ“‘
±£ђ“‘![]() ќ™ґ•µгµƒ»эљ«–ќ «µ»—ь»эљ«–ќ£Ѓ
ќ™ґ•µгµƒ»эљ«–ќ «µ»—ь»эљ«–ќ£Ѓ
[љвЈ®ћб Њ]…и÷±ѕя![]() ”л
”л![]() ÷б°Ґ
÷б°Ґ![]() ÷бЈ÷±рљї”Џµг
÷бЈ÷±рљї”Џµг![]() °Ґµг
°Ґµг![]() £ђ‘т
£ђ‘т![]() £ђ
£ђ
Љў…иіж‘Џ¬ъ„гћхЉюµƒµг![]() £ђ
£ђ
(a)µ±µг![]() ‘Џѕяґќ
‘Џѕяґќ![]() …ѕ ±£ђ»зљвЌЉҐЏЋщ Њ£ђіЋ ±µг
…ѕ ±£ђ»зљвЌЉҐЏЋщ Њ£ђіЋ ±µг![]() ”лµг
”лµг![]() ÷ЎЇѕ£ђ
÷ЎЇѕ£ђ
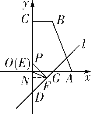
…и![]() £ђ
£ђ
‘т![]() £ђ
£ђ
![]() £ђ
£ђ
єэµг![]() „ч
„ч![]() ÷б”Џµг
÷б”Џµг![]() £ђ
£ђ
‘т![]() £ђ
£ђ
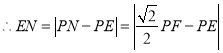 £ђ
£ђ
‘Џ![]() ÷–£ђ
÷–£ђ
![]()
![]() £ђ
£ђ
»ф![]() £ђ‘т
£ђ‘т![]() £ђљвµ√
£ђљвµ√![]() £ђє іЋ÷÷«й–ќ≤їіж‘Џ£ї
£ђє іЋ÷÷«й–ќ≤їіж‘Џ£ї
»ф![]() £ђ‘т
£ђ‘т
![]() £ђ
£ђ
’ыјнµ√![]() £ђ
£ђ
Љі![]() £ђ≤ї≥…ЅҐ£ђє іЋ÷÷«й–ќ≤їіж‘Џ£ї
£ђ≤ї≥…ЅҐ£ђє іЋ÷÷«й–ќ≤їіж‘Џ£ї
»ф![]() £ђ‘т
£ђ‘т
![]() £ђ
£ђ
’ыјнµ√![]() £ђЉі
£ђЉі![]() £ђљвµ√
£ђљвµ√![]() £Ѓ
£Ѓ
![]() £ї
£ї
(b)µ±µг![]() ‘Џ
‘Џ![]() ±я…ѕ ±£ђ»зљвЌЉҐџ£ђіЋ ±
±я…ѕ ±£ђ»зљвЌЉҐџ£ђіЋ ±![]() £ђ
£ђ
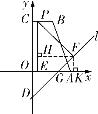
»ф![]() £ђ
£ђ
єэµг![]() Ј÷±р„ч
Ј÷±р„ч![]() ”Џµг
”Џµг![]() £ђ
£ђ![]() ÷б”Џµг
÷б”Џµг![]() £ђ
£ђ
“„÷™![]() ќ™µ»—ь÷±љ«»эљ«–ќ£ђ
ќ™µ»—ь÷±љ«»эљ«–ќ£ђ
![]() £ђ
£ђ
![]() £ђ
£ђ
°аљЂ![]() іъ»л
іъ»л![]() £ђ
£ђ
µ√![]() £ђ
£ђ
![]() £ђ
£ђ
![]() £ђ
£ђ
![]() £Ѓ
£Ѓ
(c)µ±µг![]() ‘Џѕяґќ
‘Џѕяґќ![]() …ѕ ±£ђ»зљвЌЉҐ№£ђ
…ѕ ±£ђ»зљвЌЉҐ№£ђ
![]() £ђ
£ђ
°ањ…«уµ√÷±ѕя![]() µƒљвќц љќ™
µƒљвќц љќ™
![]() £ї
£ї
Ѕ™ЅҐ![]() ”л
”л![]() £ђљвµ√
£ђљвµ√![]() £ђ
£ђ![]() £Ѓ
£Ѓ
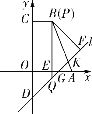
…и![]() £ђ
£ђ
‘т![]() £ђ
£ђ
![]() £ђ
£ђ
![]() £Ѓ
£Ѓ
”л(a)Ќђјн£ђњ…«уµ√
![]() £ђ
£ђ
»ф![]() £ђ‘т
£ђ‘т![]() £ђљвµ√
£ђљвµ√![]() £ђє іЋ÷÷«й–ќ≤їіж‘Џ£ї
£ђє іЋ÷÷«й–ќ≤їіж‘Џ£ї
»ф![]() £ђ‘т
£ђ‘т
![]() £ђ
£ђ
’ыјнµ√![]() £ђЉі
£ђЉі![]() £ђљвµ√
£ђљвµ√![]() £ђЈыЇѕћхЉю£ђіЋ ±
£ђЈыЇѕћхЉю£ђіЋ ±![]() £ї
£ї
»ф![]() £ђ
£ђ
‘т![]() £ђ
£ђ
’ыјнµ√![]() £ђЉі
£ђЉі![]() £ђљвµ√
£ђљвµ√![]() £ђє іЋ÷÷«й–ќ≤їіж‘Џ£ї
£ђє іЋ÷÷«й–ќ≤їіж‘Џ£ї
(d)µ±µг![]() ‘Џѕяґќ
‘Џѕяґќ![]() …ѕ ±£ђ»зљвЌЉҐЁЋщ Њ£Ѓ
…ѕ ±£ђ»зљвЌЉҐЁЋщ Њ£Ѓ
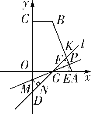
![]() µƒЉ–љ«ќ™135°г£ђ
µƒЉ–љ«ќ™135°г£ђ
°а÷їњ…ƒ№ «![]() ≥…ЅҐ£ђ
≥…ЅҐ£ђ
°аµг![]() ‘Џ
‘Џ![]() µƒ∆љЈ÷ѕя…ѕ£Ѓ
µƒ∆љЈ÷ѕя…ѕ£Ѓ
…иіЋљ«∆љЈ÷ѕя”л![]() ÷бљї”Џµг
÷бљї”Џµг![]() £ђєэµг
£ђєэµг![]() „ч
„ч![]() ÷±ѕя
÷±ѕя![]() ”Џµг
”Џµг![]() £ђ
£ђ
‘т![]() £ђ
£ђ![]() £ђ
£ђ
![]() £ђ
£ђ
љвµ√![]() £ђ
£ђ
![]() £ђ
£ђ
”÷![]() £ђ
£ђ
°а÷±ѕя![]() µƒљвќц љќ™£Ї
µƒљвќц љќ™£Ї
![]() £ђ
£ђ
Ѕ™ЅҐ÷±ѕя![]() ”л÷±ѕя
”л÷±ѕя![]() £ђ
£ђ
«уµ√![]() £ї
£ї
(e)µ±µг![]() ‘Џ
‘Џ![]() ±я…ѕ ±£ђіЋ ±
±я…ѕ ±£ђіЋ ±![]() £ђµ»—ь»эљ«–ќ≤їіж‘Џ£ї
£ђµ»—ь»эљ«–ќ≤їіж‘Џ£ї
„џ…ѕЋщ ц£ђіж‘Џ¬ъ„гћхЉюµƒµгP£ђ«“µг![]() „ш±кќ™£Ї
„ш±кќ™£Ї![]() £Ѓ
£Ѓ