Question

【题目】自我省深化课程改革以来，某校开设了：A．利用影长求物体高度，B．制作视力表，C．设计遮阳棚，D．制作中心对称图形，四类数学实践活动课．规定每名学生必选且只能选修一类实践活动课，学校对学生选修实践活动课的情况进行抽样调查，将调查结果绘制成如下两幅不完整的统计图．

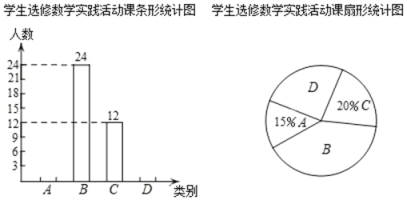
根据图中信息解决下列问题：

(1)本次共调查名学生，扇形统计图中B所对应的扇形的圆心角为度；

(2)补全条形统计图；

(3)选修D类数学实践活动的学生中有2名女生和2名男生表现出色，现从4人中随机抽取2人做校报设计，请用列表或画树状图法求所抽取的两人恰好是1名女生和1名男生的概率．

Answer 1

【答案】（1）60 ， 144（2）见解析（3）

【解析】

（1）用C类别人数除以其所占百分比可得总人数，用360°乘以C类别人数占总人数的比例即可得；
（2）总人数乘以A类别的百分比求得其人数，用总人数减去A，B，C的人数求得D类别的人数，据此补全图形即可；
（3）画树状图展示12种等可能的结果数，再找出所抽取的两人恰好是1名女生和1名男生的结果数，然后根据概率公式求解．

(1)本次调查的学生人数为12÷20%=60（名），

则扇形统计图中B所对应的扇形的圆心角为360°×=144°．

故答案为：60 , 144

(2)A类别人数为60×15%=9（人），

则D类别人数为60﹣(9+24+12)=15（人），

补全条形图如下：

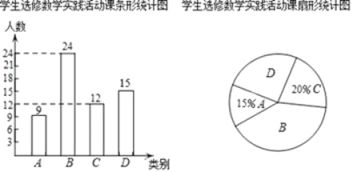
(3)画树状图为：

共有12种等可能的结果数，其中所抽取的两人恰好是1名女生和1名男生的结果数为8，所以所抽取的两人恰好是1名女生和1名男生的概率为=．