Question

【题目】如图所示，平面直角坐标系xOy中，矩形ABCD的边AB=4，BC=6．在不改变矩形ABCD的形状和大小的情况下，当矩形的顶点A在x轴的正半轴上左右移动时，另一个顶点D始终在y轴的正半轴上随之上下移动．

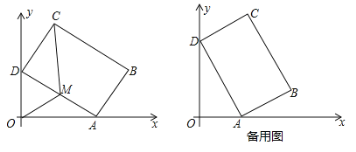
（1）当∠OAD=30°时，求点C的坐标；

（2）设AD的中点为M，连接OM、MC，若四边形OMCD的面积为时，求OA的长；

（3）在点A移动过程中是否存在某一位置，使点C到点O的距离有最大值?若存在，求此时的值；若不存在，请说明理由．

Answer 1

【答案】（1）点的坐标为；（2）；（3）存在，的最大值为8．

【解析】

(1)作CE⊥y轴，先证∠CDE＝∠OAD＝30°得CE＝CD＝2，DE＝，再由∠OAD＝30°知OD＝AD＝3，从而得出点C坐标；

(2)先求出S△DCM＝6，结合S四边形OMCD＝知S△ODM＝，S△OAD＝9，设OA＝x、OD＝y，据此知x2+y2＝36，xy＝9，得出x2+y2＝2xy，即x＝y，代入x2+y2＝36求得x的值，从而得出答案；

(3)由M为AD的中点，知OM＝3，CM＝5， OM+CM＝8，分两种情况，即当O、M、C三点不在同一条直线和三点共线时，分别进行判断解决即可.

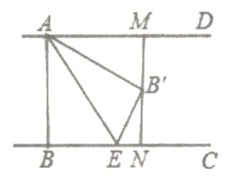
(1)如图1，过点C作CE⊥y轴于点E，

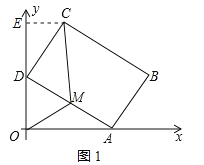
∵矩形ABCD中，CD⊥AD，

∴∠CDE+∠ADO＝90°，

又∵∠OAD+∠ADO＝90°，

∴∠CDE＝∠OAD＝30°，

∴在Rt△CED中，CE＝CD＝2，DE＝＝2，

在Rt△OAD中，∠OAD＝30°，

∴OD＝AD＝3，

∴点C的坐标为(2，3+2)；

(2)∵M为AD的中点，

∴DM＝3，S△DCM＝6，

又S边形OMCD＝，

∴S△ODM＝，

∴S△OAD＝9，

设OA＝x、OD＝y，则x2+y2＝36，xy＝9，

∴x2+y2＝2xy，即x＝y，

将x＝y代入x2+y2＝36得x2＝18，

解得x＝3 (负值舍去)，

∴OA＝3；

(3)OC的最大值为8，

如图2，M为AD的中点，

∴OM＝3，CM＝＝5，

∴OM+CM＝8.

当O、M、C三点不在同一条直线时，在△OCM中，

OC＜OM+CM＝8.

当A点运动，使得O、M、C三点在同一直线时，

此时OC= OM+CM＝8，为OC的最大值．