��Ŀ����
����Ŀ����ͼ����һ��������ԭ��O�͵�B������һ�£��õ�һ�����������ᡱ��ͼ�е�A��ʾ��11����B��ʾ10����C��ʾ18�����dzƵ�A�͵�C�����������29�����ȵ�λ������P�ӵ�A��������2��λ/����ٶ����š��������ᡱ���������˶����ӵ�O�˶�����B�ڼ��ٶȱ�Ϊԭ����һ�룬֮�����ָ̻�ԭ�٣�ͬʱ������Q�ӵ�C��������1��λ/����ٶ���������ĸ������˶����ӵ�B�˶�����O�ڼ��ٶȱ�Ϊԭ����������֮��Ҳ���ָ̻�ԭ�٣����˶���ʱ��Ϊt�룮
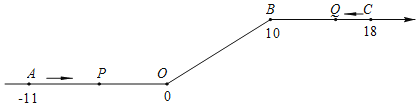
�ʣ���1������P�ӵ�A�˶���C����Ҫ����ʱ�䣿
��2��P��Q��������ʱ�����������M����Ӧ�����Ƕ��٣�
��3����tΪ��ֵʱ��P��O���������������ij�����Q��B���������������ij�����ȣ�
���𰸡���1��19.5�룻��2��M����Ӧ����Ϊ5����3��t��ֵΪ3��6.75��10.5��18
��������
��1������·�̳����ٶȵ���ʱ�䣬�ɵô𰸣�
��2����������ʱP��Q��ʱ����ȣ��ɵ÷��̣����ݽⷽ�̣��ɵô𰸣�
��3������PO��BQ��ʱ����ȣ��ɵ÷��̣����ݽⷽ�̣��ɵô𰸣�
�⣺��1����P�˶�����Cʱ������ʱ��t��11��2+10��1+8��2��19.5���룩��
�𣺶���P�ӵ�A�˶���C����Ҫ19.5ʱ�䣻
��2�������֪��P��Q�����������߶�OB����M������OM��x��
��11��2+x��1��8��1+��10��x����2��
x��5��
��M����Ӧ����Ϊ5��
��3��P��O���������������ij�����Q��B���������������ij��������4�ֿ��ܣ�
������Q��CB�ϣ�����P��AO�ϣ�
��8��t��11��2t����ã�t��3��
������Q��CB�ϣ�����P��OB�ϣ�
��8��t����t��5.5����1����ã�t��6.75��
������Q��BO�ϣ�����P��OB�ϣ�
��2��t��8������t��5.5����1����ã�t��10.5��
������Q��OA�ϣ�����P��BC�ϣ�
��10+2��t��15.5����t��13+10����ã�t��18��
����������t��ֵΪ3��6.75��10.5��18��

 ������ʱͬ����ϰ��ϵ�д�
������ʱͬ����ϰ��ϵ�д�����Ŀ��С����ϰ��������1������165��ΪĿ�꣬����20��1��������������¼���������165���IJ��ּ�Ϊ������������165���IJ��ּ�Ϊ������)
��Ŀ�������IJ�ֵ ����λ������ | ��12 | ��6 | ��2 | ��5 | ��11 |
���� | 3 | 5 | 4 | 6 | 2 |
(1)С������20��������ϰ�У�1�����������?
(2)С������20��������ϰ�У�1����������������һ�α����ٵ�һ�ζ��?
(3)С������20��������ϰ�У��ۼ��������ٸ�?
����Ŀ����![]() ��ײ�,��ÿ��
��ײ�,��ÿ��![]() ǧ��Ϊ��,��������ķֱ�������������ʾ,��¼���£�
ǧ��Ϊ��,��������ķֱ�������������ʾ,��¼���£�
��������IJ� |
|
|
|
|
|
|
�� �� |
|
|
|
|
|
|
(1)��������Ƚ�,![]() ��ײ��ܼƳ����������ǧ�ˣ�
��ײ��ܼƳ����������ǧ�ˣ�
(2)���ײ�ÿǧ���ۼ�![]() Ԫ,�������
Ԫ,�������![]() ��ײ˿�������Ԫ��
��ײ˿�������Ԫ��





