题目内容
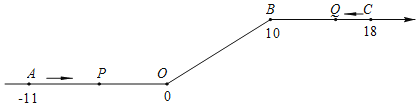
【题目】如图，在△ABC中，AB=AC，AD平分∠BAC，CE∥AD且CE=AD.
（1）求证：四边形ADCE是矩形；
（2）若△ABC是边长为
的等边三角形，AC，DE相交于点O，在CE上截取CF=CO，连接OF，求线段FC的长及四边形AOFE的面积.
【答案】（1）证明见解析；（2）
.
【解析】
试题（1）根据平行四边形判定得出平行四边形，再根据矩形判定推出即可.
（2）分别求出AE、OH、CE、CF的长，再求出三角形AEC和三角形COF的面积，即可求出答案．
试题解析：（1）∵CE∥AD且CE=AD，∴四边形ADCE是平行四边形.
∵AD⊥BC，∴∠ADC=90°.
∴四边形ADCE是矩形.
（2）∵△ABC是等边三角形，边长为4，∴AC=4，∠DAC=30°.
∴∠ACE=30°，AE=2，CE=
.
∵四边形ADCE为矩形，∴OC=OA=2.
∵CF=CO，∴CF=2.
如图，过O作OH⊥CE于H，
∴OE=
OC=1.
∴
.
【题目】山地自行车越来越受到中学生的喜爱，各种品牌相继投放市场，某车行经营的A型车去年销售总额为5万元，今年每辆售价比去年降低400元，若卖出的数量相同，销售总额将比去年减少20%．
A，B两种型号车的进货和销售价格如下表：
A型车 | B型车 | |
进货价格（元） | 1 100 | 1 400 |
销售价格（元） | 今年的销售价格 | 2 000 |
（1）今年A型车每辆售价多少元？（用列方程的方法解答）
（2）该车行计划新进一批A型车和新款B型车共60辆，且B型车的进货数量不超过A型车数量的两倍，应如何进货才能使这批车获利最多？
【题目】某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查，绘制出频数分布表和频数分布直方图的一部分．
请根据图表信息回答下列问题：
视力 | 频数（人） | 频率 |
4.0≤x＜4.3 | 20 | 0.1 |
4.3≤x＜4.6 | 40 | 0.2 |
4.6≤x＜4.9 | 70 | 0.35 |
4.9≤x＜5.2 | a | 0.3 |
5.2≤x＜5.5 | 10 | b |
（1）本次调查的样本为________，样本容量为_______；
（2）在频数分布表中，a=______，b=______，并将频数分布直方图补充完整；
（3）若视力在4.6以上（含4.6）均属正常，根据上述信息估计全区初中毕业生中视力正常的学生有多少人？
【题目】为了解某区初二年级数学学科期末质量监控情况，进行了抽样调查，过程如下，请将有关问题补充完整．
收集数据：随机抽取甲乙两所学校的20名学生的数学成绩进行分析：
甲 | 91 | 89 | 77 | 86 | 71 | 31 | 97 | 93 | 72 | 91 |
81 | 92 | 85 | 85 | 95 | 88 | 88 | 90 | 44 | 91 | |
乙 | 84 | 93 | 66 | 69 | 76 | 87 | 77 | 82 | 85 | 88 |
90 | 88 | 67 | 88 | 91 | 96 | 68 | 97 | 59 | 88 |
整理、描述数据：按如下数据段整理、描述这两组数据
分段 学校 | 30≤x≤39 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 1 | 1 | 0 | 0 | 3 | 7 | 8 |
乙 |
|
|
|
|
|
|
|
分析数据：两组数据的平均数、中位数、众数、方差如下表：
统计量 学校 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 81.85 | 88 | 91 | 268.43 |
乙 | 81.95 | 86 | m | 115.25 |
经统计，表格中m的值是 ．
得出结论：
a若甲学校有400名初二学生，估计这次考试成绩80分以上人数为 ．
b可以推断出 学校学生的数学水平较高，理由为 ．（至少从两个不同的角度说明推断的合理性）
【题目】如图，在△ABC中，∠C=60°，BC=3厘米，AC=4厘米，点P从点B出发，沿B→C→A以每秒1厘米的速度匀速运动到点A．设点P的运动时间为x秒，B、P两点间的距离为y厘米．
小新根据学习函数的经验，对函数
随自变量
的变化而变化的规律进行了探究．
下面是小新的探究过程，请补充完整：
（1）通过取点、画图、测量，得到了x与y的几组值，如下表：
x（s） | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
y（cm） | 0 | 1.0 | 2.0 | 3.0 | 2.7 | 2.7 | m | 3.6 |
经测量m的值是（保留一位小数）．
（2）建立平面直角坐标系，描出表格中所有各对对应值为坐标的点，画出该函数的图象；
（3）结合画出的函数图象，解决问题：在曲线部分的最低点时，在△ABC中画出点P所在的位置．
