题目内容
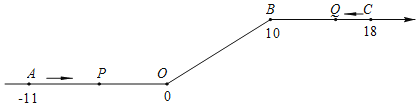
【题目】某烟机零件加工车间，甲组工人加工零件，工作中有一次停产检修机器，然后继续加工．由于任务紧急，乙组工人加入，与甲组工人一起生产零件．两组各自加工零件的数量y（个）与甲组工人加工时间t（时）之间的函数图象如图所示．
（l）求乙组加工零件的数量y与时间t之间的函数关系式．
（2）求甲组加工零件总量a．
【答案】(1) y=120x﹣600；(2)280个.
【解析】分析：(1)由图象可知，乙组加工零件的数量y与时间t之间是一次函数的关系，函数图象过点(5，0)，(8，360)，用待定系数法求y与t之间的函数关系式；(2)把x＝7代入(1)所求的函数关系式求出x＝7时，y的值，即可得到甲在4时到8时之间每小时加工的零件数量，由此求出8小时时加工的零件数量.
详解：解：(1)当0≤t＜5时，y＝0，
当5≤t≤8时，设y与时间t之间的函数关系式为：y＝kx＋b，
将(5，0)，(8，360)代入得：
，解得：
，
∴y与时间t之间的函数关系式为：y＝120x﹣600；
(2)∵当t＝7时，y＝120×7﹣600＝240，
4时到8时之间每小时加工的零件数量为(240﹣120)÷(7﹣4)＝40.
∴a＝120＋40×(8﹣4)＝280(个).
阅读快车系列答案【题目】山地自行车越来越受到中学生的喜爱，各种品牌相继投放市场，某车行经营的A型车去年销售总额为5万元，今年每辆售价比去年降低400元，若卖出的数量相同，销售总额将比去年减少20%．
A，B两种型号车的进货和销售价格如下表：
A型车 | B型车 | |
进货价格（元） | 1 100 | 1 400 |
销售价格（元） | 今年的销售价格 | 2 000 |
（1）今年A型车每辆售价多少元？（用列方程的方法解答）
（2）该车行计划新进一批A型车和新款B型车共60辆，且B型车的进货数量不超过A型车数量的两倍，应如何进货才能使这批车获利最多？
【题目】如图，在△ABC中，∠C=60°，BC=3厘米，AC=4厘米，点P从点B出发，沿B→C→A以每秒1厘米的速度匀速运动到点A．设点P的运动时间为x秒，B、P两点间的距离为y厘米．
小新根据学习函数的经验，对函数
随自变量
的变化而变化的规律进行了探究．
下面是小新的探究过程，请补充完整：
（1）通过取点、画图、测量，得到了x与y的几组值，如下表：
x（s） | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
y（cm） | 0 | 1.0 | 2.0 | 3.0 | 2.7 | 2.7 | m | 3.6 |
经测量m的值是（保留一位小数）．
（2）建立平面直角坐标系，描出表格中所有各对对应值为坐标的点，画出该函数的图象；
（3）结合画出的函数图象，解决问题：在曲线部分的最低点时，在△ABC中画出点P所在的位置．
