题目内容
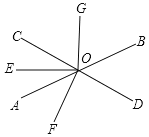
【题目】已知点O为直线AB上一点,将直角三角板MON的直角顶点放在点O处,并在∠MON内部作射线OC.
(1)将三角板放置到如图所示位置,使OC恰好平分∠MOB,且∠BON=2∠NOC,求∠AOM的度数;
(2)若仍将三角板按照如图所示的方式放置,仅满足OC平分∠MOB,试猜想∠AOM与∠NOC之间的数量关系,并说明理由.

【答案】(1)45°;(2)∠AOM=2∠NOC,理由见解析..
【解析】
(1)由∠BON=2∠NOC,OC平分∠MOB可得∠MOC=∠BOC=3∠NOC,然后利用角的倍分关系即可求解;
(2)令∠NOC为β,∠AOM为γ,∠MOC=90°-β,根据∠AOM+∠MOC+∠BOC=180°即可得到∠AOM与∠NOC满足的数量关系.
解:(1)∵∠BON=2∠NOC,OC平分∠MOB,
∴∠MOC=∠BOC=3∠NOC,
∵∠MOC+∠NOC=∠MON=90°,
∴3∠NOC+∠NOC=90°,
∴4∠NOC=90°,
∴∠BON=2∠NOC=45°,
∴∠AOM=180°﹣∠MON﹣∠BON=180°﹣90°﹣45°=45°;
(2)∠AOM=2∠NOC.
令∠NOC为β,∠AOM为γ,∠MOC=90°﹣β,
∵∠AOM+∠MOC+∠BOC=180°,
∴γ+90°﹣β+90°﹣β=180°,
∴γ﹣2β=0,即γ=2β,
∴∠AOM=2∠NOC.

【题目】暑假到了,即将迎来手机市场的销售旺季.某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
甲 | 乙 | |
进价(元/部) | 4000 | 2500 |
售价(元/部) | 4300 | 3000 |
该商场计划投入15.5万元资金,全部用于购进两种手机若干部,期望全部销售后可获毛利润不低于2万元.(毛利润=(售价﹣进价)×销售量)
(1)若商场要想尽可能多的购进甲种手机,应该安排怎样的进货方案购进甲乙两种手机?
(2)通过市场调研,该商场决定在甲种手机购进最多的方案上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
【题目】山地自行车越来越受到中学生的喜爱,各种品牌相继投放市场,某车行经营的A型车去年销售总额为5万元,今年每辆售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
A,B两种型号车的进货和销售价格如下表:
A型车 | B型车 | |
进货价格(元) | 1 100 | 1 400 |
销售价格(元) | 今年的销售价格 | 2 000 |
(1)今年A型车每辆售价多少元?(用列方程的方法解答)
(2)该车行计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?