题目内容
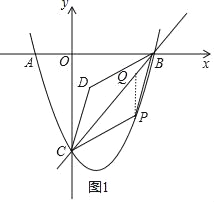
【题目】如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C,作直线BC,点P是抛物线上一个动点(点P不与点B,C重合),连结PB,PC,以PB,PC为边作CPBD,设CPBD的面积为S,点P的横坐标为m.
(1)求抛物线对应的函数表达式;
(2)当点P在第四象限,且CPBD有两个顶点在x轴上时,求点P的坐标;
(3)求S与m之间的函数关系式;
(4)当x轴将CPBD的面积分成1:7两部分时,直接写出m的值.

【答案】(1)y=x2﹣2x﹣3;(2)(2,﹣3); (3)S=3m2﹣9m;
(4)m的值为1或1+![]() 或1﹣
或1﹣![]() .
.
【解析】试题分析:(1)利用交点式求抛物线的解析式;
(2)先确定点D在x轴上,再利用平行四边形的性质可判断PC∥x轴,然后根据抛物线的对称性确定点P的坐标;
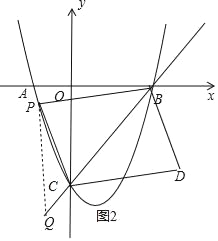
(3)作PQ∥y轴交直线BC于Q,如图1,利用待定系数法求出直线BC的解析式为y=x-3,设P(m,m2-2m-3),则Q(m,m-3),讨论:当0<m<3时,如图1,PQ=-m2+3m,利用三角形面积公式和平行四边形的性质得S=2S△PBC=2(S△PQC+S△PQB)=-3m2+9m;当m<0或m>3时,如图2,PQ=m2-3m,同理可得S=2S△PBC=2(S△PBQ-S△PQC)=3m2-9m;
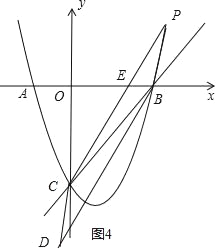
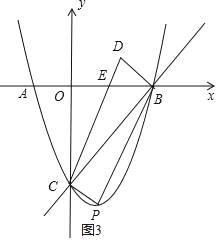
(4)讨论:当点P在x轴下方,如图3,CD交x轴于E,利用已知条件得到S△DEB:S平行四边形CPBD=1:8,再根据平行四边形的性质得S△DEB:S△BCE=1:3,接着根据三角形面积公式得到D点的纵坐标为1,然后利用点平移的坐标规律得到点C向下平移1个单位可得到P点,即P点的纵坐标为-4,则解方程x2-2x-3=-4可得到对应m的值;当点P在x轴上方,如图4,CP交x轴于E,同理可得点P到x轴的距离为1,即P点的纵坐标为1,则通过解方程x2-2x-3=1可得对应m的值.
解:(1)抛物线的解析式为y=(x+1)(x﹣3),
即y=x2﹣2x﹣3;
(2)∵CPBD有两个顶点在x轴上,
∴点D在x轴上,
而BD∥PC,
∴点P和点C为抛物线上的对称点,
而抛物线的对称轴为直线x=1,
∴点P的坐标为(2,﹣3);
(3)作PQ∥y轴交直线BC于Q,如图1,
设直线BC的解析式为y=kx+b,
把C(0,﹣3),B(3,0)代入得![]() ,解得
,解得![]() ,
,
∴直线BC的解析式为y=x﹣3,
设P(m,m2﹣2m﹣3),则Q(m,m﹣3),
当0<m<3时,如图1,PQ=m﹣3﹣(m2﹣2m﹣3)=﹣m2+3m
S=2S△PBC=2(S△PQC+S△PQB)=2![]() 3(﹣m2+3m)=﹣3m2+9m;
3(﹣m2+3m)=﹣3m2+9m;
当m<0或m>3时,如图2,PQ=m2﹣2m﹣3﹣(m﹣3)=m2﹣3m
S=2S△PBC=2(S△PBQ﹣S△PQC)=2![]() 3(m2﹣3m)=3m2﹣9m;
3(m2﹣3m)=3m2﹣9m;
(4)当点P在x轴下方,如图3,CD交x轴于E,
∵x轴将CPBD的面积分成1:7两部分,
∴S△DEB:S平行四边形CPBD=1:8,
∴S△DEB:S△BCD=1:4,
∴S△DEB:S△BCE=1:3,
而OC=3,
∴点D到x轴的距离为1,即D点的纵坐标为1,
∵四边形CPBD为平行四边形,
∴点C向下平移1个单位可得到P点,即P点的纵坐标为﹣4,
当x=﹣4时,x2﹣2x﹣3=﹣4,解得x1=x2=1,则P点坐标为(1,﹣4),
∴m=1;
当点P在x轴上方,如图4,CP交x轴于E,
∵x轴将CPBD的面积分成1:7两部分,
∴S△PEB:S平行四边形CPBD=1:8,
∴S△PEB:S△BCP=1:4,
∴S△PEB:S△BCE=1:3,
而OC=3,
∴点P到x轴的距离为1,即P点的纵坐标为1,
当y=1时,x2﹣2x﹣3=1,解得x1=1+![]() ,x2=1﹣
,x2=1﹣![]() ,则P点坐标为(1+
,则P点坐标为(1+![]() ,1)或(1﹣
,1)或(1﹣![]() ,1),
,1),
∴m=1+![]() 或m=1﹣
或m=1﹣![]() ,
,
综上所述,m的值为1或1+![]() 或1﹣
或1﹣![]() .
.

【题目】![]() 开通了,中国联通公布了资费标准,其中包月186元时,超出部分国内拨打0.36元/分.由于业务多,小明的爸爸打电话已超出了包月费.下表是超出部分国内拨打的收费标准.
开通了,中国联通公布了资费标准,其中包月186元时,超出部分国内拨打0.36元/分.由于业务多,小明的爸爸打电话已超出了包月费.下表是超出部分国内拨打的收费标准.
时间/分 | 1 | 2 | 3 | 4 | 5 | … |
电话费/元 | 0.36 | 0.72 | 1.08 | 1.44 | 1.80 | … |
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?
(2)如果用x表示超出时间,y表示超出部分的电话费,那么y与x的关系式是什么?
(3)如果打电话超出![]() 分钟,需多付多少电话费?
分钟,需多付多少电话费?
(4)某次打电话的费用超出部分是![]() 元,那么小明的爸爸打电话超出几分钟?
元,那么小明的爸爸打电话超出几分钟?