题目内容
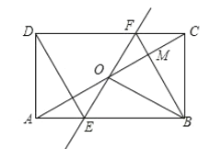
【题目】已知:直线EF//MN,点A、B分别为EF,MN上的动点,且∠ACB= a,BD平分∠CBN交EF于D.
(1)若∠FDB=120°,a=90°.如图1,求∠MBC与∠EAC的度数?
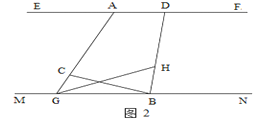
(2)延长AC交直线MN于G,这时a =80°,如图2,GH平分∠AGB交DB于点H,问∠GHB是否为定值,若是,请求值.若不是,请说明理由?


【答案】(1)60°,30°;(2)为定值50°.
【解析】
(1)过C作CP∥EF,进而得到EF∥MN∥CP,根据平行线的性质,求出∠DBN的度数,进而求出∠MBC、∠EAC的度数;
(2)根据∠CBN是△CBG的外角,得到∠BCG=∠CBN﹣∠AGB.根据角平分线的定义得到∠HGB![]() ∠AGB,∠DBN
∠AGB,∠DBN![]() ∠CBN.由三角形外角的性质得到∠GHB=∠DBN﹣∠HGB
∠CBN.由三角形外角的性质得到∠GHB=∠DBN﹣∠HGB![]() ∠CBN
∠CBN![]() ∠AGB
∠AGB![]() (∠CBN﹣∠AGB)
(∠CBN﹣∠AGB)![]() ∠BCG,即可得出结论.
∠BCG,即可得出结论.
(1)如图1,过C作CP∥EF.
∵EF∥MN,∴EF∥MN∥CP.
∵EF∥MN,∴∠NBD=180°-∠FDB=180°-120°=60°.
∵BD平分∠CBN,∴∠CBD=∠NBD=60°,∴∠MBC=180°-∠CBD-∠NBD=180°-60°-60°=60°.
∵CP∥MN,∴∠PCB=∠MBC=60°,∴∠ACP=∠ACB-∠BCP=90°-60°=30°.
∵EF∥CP,∴∠EAC=∠ACP=30°.

(2)∠GHB为定值50°.理由如下:
∵∠CBN是△CBG的外角,∴∠BCG=∠CBN﹣∠AGB.
∵GH平分∠AGB,BD平分∠CBN,∴∠HGB![]() ∠AGB,∠DBN
∠AGB,∠DBN![]() ∠CBN.
∠CBN.
∵∠DBN是△HGB的外角,∴∠GHB=∠DBN﹣∠HGB![]() ∠CBN
∠CBN![]() ∠AGB
∠AGB![]() (∠CBN﹣∠AGB)
(∠CBN﹣∠AGB)![]() ∠BCG
∠BCG![]() (180°-80°)=50°,故∠GHB是定值50°.
(180°-80°)=50°,故∠GHB是定值50°.

 走进文言文系列答案
走进文言文系列答案