题目内容
【题目】认真阅读下面的材料,完成有关问题.
材料:在学习绝对值时,老师教过我们绝对值的几何含义,如![]() 表示
表示![]() 、
、![]() 在数轴上对应的两点之间的距离;
在数轴上对应的两点之间的距离;![]() ,所以
,所以![]() 表示
表示![]() 、
、![]() 在数轴上对应的两点之间的距离;
在数轴上对应的两点之间的距离;![]() ,所以
,所以![]() 表示
表示![]() 在数轴上对应的点到原点的距离.
在数轴上对应的点到原点的距离.
一般地,点![]() 、点
、点![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() 、
、![]() ,那么点
,那么点![]() 、点
、点![]() 之间的距离可表示为
之间的距离可表示为![]() .
.
(1)点![]() 、
、![]() 、
、![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() 、
、![]() 、
、![]() ,那么点
,那么点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到点
到点![]() 的距离之和可表示为__________(用含绝对值的式子表示).
的距离之和可表示为__________(用含绝对值的式子表示).
(2)利用数轴探究:
①满足![]() 的
的![]() 的取值范围是__________.
的取值范围是__________.
②满足![]() 的
的![]() 的所有值是__________.
的所有值是__________.
③设![]() ,当
,当![]() 的值取在不小于
的值取在不小于![]() 且不大于
且不大于![]() 的范围时,
的范围时,![]() 的值是不变的,而且是
的值是不变的,而且是![]() 的最小值,这个最小值是_____.
的最小值,这个最小值是_____.
(3)拓展:
①![]() 的最小值为__________.
的最小值为__________.
②![]() 的最小值为__________.
的最小值为__________.
③![]() 的最小值为__________,此时
的最小值为__________,此时![]() 的取值范围为__________.
的取值范围为__________.
【答案】(1)|x+2|+|x1|;(2)①-2≤x≤1,②-3,2,③8;(3)①1,②2,③1020100,![]() .
.
【解析】
(1)根据绝对值的几何含义,可得答案;
(2)①②③根据绝对值的几何含义结合数轴解答即可;
(3)①由(2)可知当x在不小于1且不大于2的范围时,![]() 取最小值;
取最小值;
②由(2)可知要使|x1|+|x-3|的值最小,x的值取1到3之间(包括1、3)的任意一个数,要使|x2|的值最小,x应取2,显然当x=2时能同时满足要求,把x=2代入原式计算即可;
③由(2)可知x的值取1010到1011之间(包括1010、1011)的任意一个数时,![]() 取最小值且值是不变的,然后计算即可.
取最小值且值是不变的,然后计算即可.
(1)A到B的距离与A到C的距离之和可表示为:|x+2|+|x1|;
(2)①![]() 的几何意义是x到-2和1的距离之和等于3,所以x在-2和1之间,即:-2≤x≤1;
的几何意义是x到-2和1的距离之和等于3,所以x在-2和1之间,即:-2≤x≤1;
②![]() 的几何意义是x到-2和1的距离之和等于5,所以在数轴上,当x在-2左侧时,x=-2-1=-3,当x在1右侧时,x=1+1=2,故x的所有值是:-3,2;
的几何意义是x到-2和1的距离之和等于5,所以在数轴上,当x在-2左侧时,x=-2-1=-3,当x在1右侧时,x=1+1=2,故x的所有值是:-3,2;
③当![]() 的值取在不小于
的值取在不小于![]() 且不大于
且不大于![]() 的范围时,即在数轴上,x在-3和5之间,而p表示x到-3和5的距离之和,所以此时p是:8.
的范围时,即在数轴上,x在-3和5之间,而p表示x到-3和5的距离之和,所以此时p是:8.
(3)①由(2)可知当x在不小于1且不大于2的范围时,![]() 取最小值,此时最小值为:1;
取最小值,此时最小值为:1;
②由(2)可知要使|x1|+|x-3|的值最小,x的值取1到3之间(包括1、3)的任意一个数,要使|x2|的值最小,x应取2,显然当x=2时能同时满足要求,所以![]() 的最小值为:2;
的最小值为:2;
③由(2)可知x的值取1010到1011之间(包括1010、1011)的任意一个数时,![]() 取最小值且值是不变的,假设x=1010,则最小值为:
取最小值且值是不变的,假设x=1010,则最小值为:![]()
![]() ,此时
,此时![]() 的取值范围为:
的取值范围为:![]()

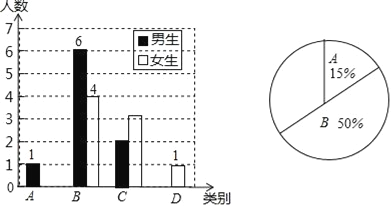
【题目】我市举行“第十七届中小学生书法大赛”作品比赛,已知每幅参赛作品成绩记为![]() ,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
分数段 | 频数 | 百分比 |
| 38 | 0.38 |
|
| 0.32 |
|
|
|
| 10 | 0.1 |
合计 | 100 | 1 |
书法作品比赛成绩频数直方图

根据上述信息,解答下列问题:
(1)请你把表中空白处的数据填写完整.
(2)请补全书法作品比赛成绩频数直方图.
(3)若80分(含80分)以上的书法作品将被评为等级奖,试估计全市获得等级的幅数.