Question

【题目】如图，AB是半圆O的直径，半径OC⊥AB于O，AD平分∠CAB交于点D，连接CD，OD，BD．下列结论中正确的是（ ）

A.AC∥ODB.

C.△ODE∽△ADOD.

Answer 1

【答案】A

【解析】

A.根据等腰三角形的性质和角平分线的性质，利用等量代换求证∠CAD=∠ADO即可；
B.过点E作EF⊥AC，根据角平分线上的点到角的两边的距离相等可得OE=EF，再根据直角三角形斜边大于直角边可证；
C.两三角形中，只有一个公共角的度数相等，其它两角不相等，所以不能证明③△ODE∽△ADO；
D.根据角平分线的性质得出∠CAD=∠BAD，根据在同圆或等圆中，相等的圆周角所对的弦相等，可得CD=BD，又因为CD+BD>BC,又由AC=BC可得AC<2CD，从而可判断D错误．

解：解：A.∵AB是半圆直径，
∴AO=OD，
∴∠OAD=∠ADO，
∵AD平分∠CAB交弧BC于点D，
∴∠CAD=∠DAO= ∠CAB，
∴∠CAD=∠ADO，
∴AC∥OD，
∴A正确．
B.如图，过点E作EF⊥AC，

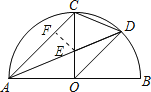
∵OC⊥AB，AD平分∠CAB交弧BC于点D，
∴OE=EF，
在Rt△EFC中，CE＞EF，
∴CE＞OE，
∴B错误．
C.∵在△ODE和△ADO中，只有∠ADO=∠EDO，
∵∠COD=2∠CAD=2∠OAD，
∴∠DOE≠∠DAO，
∴不能证明△ODE和△ADO相似，
∴C错误；

D.∵AD平分∠CAB交于点D，

∴∠CAD=∠BAD.

∴CD=BD

∴BC<CD+BD=2CD,

∵半径OC⊥AB于O，

∴AC=BC,

∴AC<2CD，

∴D错误.

故选A.