题目内容
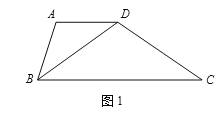
【题目】如图,AD是⊙O的直径,BA=BC,BD交AC于点E,点F在DB的延长线上,且∠BAF=∠C.
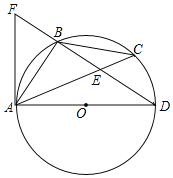
(1)求证:AF是⊙O的切线;
(2)若BC=2![]() ,BE=4,求⊙O半径r.
,BE=4,求⊙O半径r.
【答案】(1)见解析;(2)![]()
【解析】
(1)由圆周角定理得出∠ABD=90°,∠C=∠D,证出∠BAD+∠BAF=90°,得出AF⊥AD,即可得出结论;
(2)由圆周角定理得出∠BAC=∠C,∠C=∠D,得出∠BAC=∠D,再由公共角∠ABE=∠DBA,即可得出△ABE∽△DBA,求出AB长,由勾股定理可求出AD长,则⊙O半径可求出.
(1)证明:∵AD是⊙O的直径,
∴∠ABD=90°,
∴∠BAD+∠D=90°,
∵∠BAF=∠C,∠C=∠D,
∴∠BAF=∠D,
∴∠BAD+∠BAF=90°,
即∠FAD=90°,
∴AF⊥AD,
∴AF是⊙O的切线;
(2)解:∵AB=BC,
∴![]() ,
,
∴∠BAC=∠C,
∵∠C=∠D,
∴∠BAC=∠D,即∠BAE=∠D,
又∵∠ABE=∠DBA,
∴△ABE∽△DBA;
∴![]() ,
,
∴AB2=BDBE,
∵AB=BC=2![]() ,BE=4,
,BE=4,
∴BD=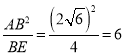 ,
,
∴AD![]() ,
,
∴⊙O半径r=![]() .
.

练习册系列答案
相关题目
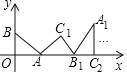
【题目】我们把如图1所示的菱形称为基本图形,将此基本图形不断复制并平移,使得相邻两个基本图形的一个顶点与对称中心重合,得到的所有菱形都称为基本图形的特征图形,显然图2中有3个特征图形.

(1)观察以上图形并完成如表:
根据表中规律猜想,图n(n≥2)中特征图形的个数为 .(用含n的式子表示)
图形名称 | 基本图形的个数 | 特征图形的个数 |
图1 | 1 | 1 |
图2 | 2 | 3 |
图3 | 3 | 7 |
图4 | 4 | |
…… | …… | …… |
(2)若基本图形的面积为2,则图2中小特征图形的面积是 ;图2020中所有特征图形的面积之和为 .