题目内容
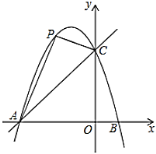
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的顶点为P,且与y轴交于点A,与直线
的顶点为P,且与y轴交于点A,与直线![]() 交于点B,C(点B在点C的左侧).
交于点B,C(点B在点C的左侧).
(1)求抛物线![]() 的顶点P的坐标(用含a的代数式表示);
的顶点P的坐标(用含a的代数式表示);
(2)横、纵坐标都是整数的点叫做整点,记抛物线与线段AC围成的封闭区域(不含边界)为“W区域”.
①当![]() 时,请直接写出“W区域”内的整点个数;
时,请直接写出“W区域”内的整点个数;
②当“W区域”内恰有2个整点时,结合函数图象,直接写出a的取值范围.
【答案】(1)顶点P的坐标为![]() ;(2)① 6个;②
;(2)① 6个;② ![]() ,
,![]() .
.
【解析】
(1)由抛物线解析式直接可求;
(2)①由已知可知A(0,2),C(2+![]() ,-2),画出函数图象,观察图象可得;
,-2),画出函数图象,观察图象可得;
②分两种情况求:当a>0时,抛物线定点经过(2,-2)时,a=1,抛物线定点经过(2,-1)时,a=![]() ,则
,则![]() <a≤1;当a<0时,抛物线定点经过(2,2)时,a=-1,抛物线定点经过(2,1)时,a=-
<a≤1;当a<0时,抛物线定点经过(2,2)时,a=-1,抛物线定点经过(2,1)时,a=-![]() ,则-1≤a<-
,则-1≤a<-![]() .
.
解:(1)∵y=ax2-4ax+2a=a(x-2)2-2a,
∴顶点为(2,-2a);
(2)如图,①∵a=2,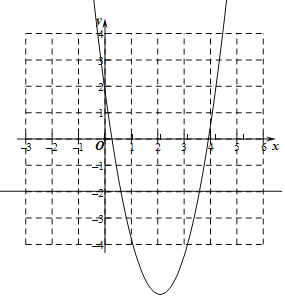
∴y=2x2-8x+2,y=-2,
∴A(0,2),C(2+![]() ,-2),
,-2),
∴有6个整数点;
②当a>0时,抛物线定点经过(2,-2)时,a=1,
抛物线定点经过(2,-1)时,,![]() ;
;
∴ ![]() .
.
当![]() 时,抛物线顶点经过点(2,2)时,
时,抛物线顶点经过点(2,2)时,![]() ;
;
抛物线顶点经过点(2,1)时,![]() ;
;
∴ ![]() .
.
∴综上所述:![]() ,
,![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目