题目内容
【题目】在![]() 中,
中,![]() , 记
, 记![]() ,点
,点![]() 为射线
为射线![]() 上的动点,连接
上的动点,连接![]() ,将射线
,将射线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 角后得到射线
角后得到射线![]() ,过点
,过点![]() 作
作![]() 的垂线,与射线
的垂线,与射线![]() 交于点
交于点![]() ,点
,点![]() 关于点
关于点![]() 的对称点为
的对称点为![]() ,连接
,连接![]() .
.
(1)当![]() 为等边三角形时,
为等边三角形时,
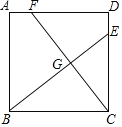
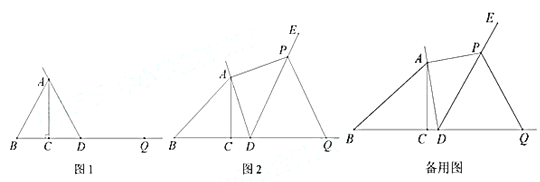
① 依题意补全图1;
②![]() 的长为________;
的长为________;
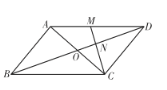
(2)如图2,当![]() ,且
,且![]() 时, 求证:
时, 求证:![]() ;
;
(3)设![]() , 当
, 当![]() 时,直接写出
时,直接写出![]() 的长. (用含
的长. (用含![]() 的代数式表示)
的代数式表示)
【答案】(1)①见解析,②![]() . (2)见解析;(3)
. (2)见解析;(3)![]() .
.
【解析】
(1)①根据题意补全图形即可;
②根据旋转的性质和对称的性质易证得![]() ,利用特殊角的三角函数值即可求得答案;
,利用特殊角的三角函数值即可求得答案;
(2)作![]() 于
于![]() ,
,![]() 于
于![]() ,证得四边形
,证得四边形![]() 是矩形,求得
是矩形,求得![]() ,再证得
,再证得![]() ,求得
,求得![]() ,再求得
,再求得![]() ,即可证得结论.
,即可证得结论.
(3)设![]() 则
则![]() ,证得
,证得![]() ,求得
,求得![]() ,再作DM⊥AB,PN⊥DQ,利用面积法求得
,再作DM⊥AB,PN⊥DQ,利用面积法求得![]() ,继而求得
,继而求得![]() ,再证得
,再证得![]() ,求得
,求得![]() ,根据
,根据![]() 得
得![]() ,即可求得答案.
,即可求得答案.
(1)解:①补全图形如图所示:
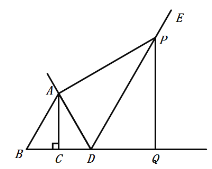
②∵![]() 为等边三角形,
为等边三角形,
∴![]() ,
,![]() ,
,
根据旋转的性质和对称的性质知:![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,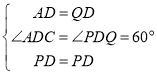 ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 为等边三角形,
为等边三角形,![]() ,
,
∴ ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)作![]() 于
于![]() ,
,![]() 于
于![]() ,
,
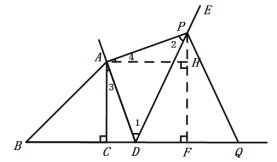
∵![]() ,
,
∴![]() ,
,
由题意可知![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() 关于点
关于点![]() 对称,
对称,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 为
为![]() 中点,
中点,
∴![]() 垂直平分
垂直平分![]() ,
,
∴![]() ;
;
(3)∵![]() ,AC⊥BD,
,AC⊥BD,
∴![]() ,
,
设![]() 则
则![]() ,
,
∵AC⊥BD,AP⊥AD,
∴∠ACB=∠PAD![]() ,
,
又∵∠ABC=∠PDA![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴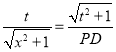 ,
,
∴![]() ,
,
作DM⊥AB,PN⊥DQ,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴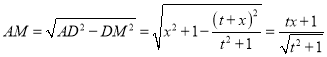 ,
,
∵![]() ,
,
又∵∠AB![]() =∠PDA
=∠PDA![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴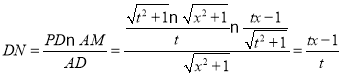 ,
,
∵![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴![]() .
.


练习册系列答案
相关题目