Question

【题目】如图，四边形是菱形，且，点是对角线上一点，，绕点逆时针旋转射线，旋转角度为，并交射线于点，连接，，，

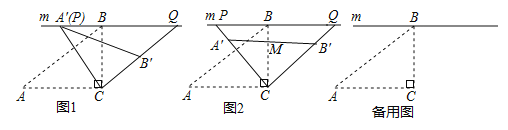
（1）①当时，补全图形，并证明；

②当时，直接写出线段，，之间的关系；

（2）在平面上找到一点，使得对于任意的，总有，直接写出点的位置．

（3）选择下面任意一问回答即可（全卷最多不超过100分）

A．证明（1）②的结论．

B．根据（2）中找到的的位置，证明

Answer 1

【答案】（1）①见解析；（1）②；（2）过点G作AG的垂线与AG绕点A顺时针针旋转的交点为k；（3）见解析

【解析】

（1）①连接EB，通过AAS证△CBE≌△EBG；

（1）②将ED转化为EB，EC转化为BG，在Rt△EGB中得到线段直角的关系；

（2）构造含30°的Rt△AGK，即可得到结论；

（3）前2问已证明

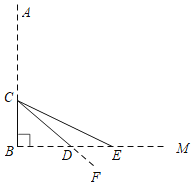
(1)①图形如下,连接BE

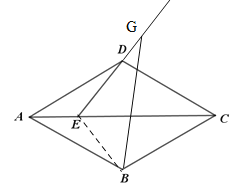
∵四边形ABCD是菱形,∠BAD=60°

∴∠DCE=∠BCE=30°

∵∠DEC=∠GBC =50°

∴根据菱形的对称性∠BEC=50°,

在△BCE中,

∴∠EBG=180°-∠BCE-∠GBC-∠BEC=50°=∠GEB

∴在△EDC中,∠EDC=100°

∴在四边形ADCB中,∠EBC=100°,∴∠BEC=∠EBG

∵BE=BE

∴△CBE≌△EBG

∴EG=BC

②

（2）如下图，过点G作AG的垂线，交AC于点M，顺时针旋转AG至AK处，使得∠GAD=∠KAC，AK与GM的交点为点K

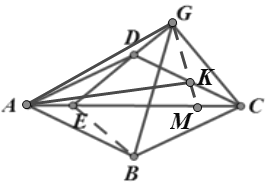
（3）A.

根据菱形的对称性,ED=EB,∠BEC=∠DEC=45°

∴∠GEB=90°,△GEB是直角三角形

∵∠BGE=∠BCE=30°，

则有EG= ,

过B点作BH⊥CE于点H，

∵∠CEB=45°，∠ECB=30°，

∴

∴

B.

∵∠DAC=30°，∠GAD=∠KAC

∴∠GAK=30°

∵AG⊥GM

∴△AGK是直角三角形，且∠GAK=30°

∴