题目内容
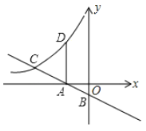
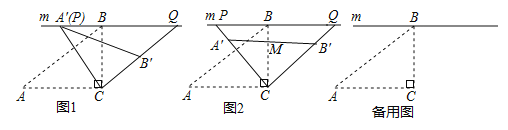
【题目】在![]() 中,
中,![]() ,过点
,过点![]() 作直线
作直线![]() ,将
,将![]() 绕点C顺时针旋转得到
绕点C顺时针旋转得到![]() (点
(点![]() 的对应点分别是
的对应点分别是![]() ),射线
),射线![]() 分别交直线
分别交直线![]() 于点
于点![]() .
.
(1)问题发现:如图1所示,若![]() 与
与![]() 重合,则
重合,则![]() 的度数为_________________
的度数为_________________
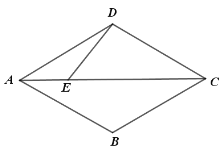
(2)类比探究:如图2,所示,设![]() 与
与![]() 的交点为M,当M为
的交点为M,当M为![]() 中点时,求线段
中点时,求线段![]() 的长;
的长;
(3)拓展延伸:在旋转过程中,当点![]() 分别在
分别在![]() 的延长线上时,试探究四边形
的延长线上时,试探究四边形![]() 的面积是否存在最小值,若存在,直接写出四边形
的面积是否存在最小值,若存在,直接写出四边形![]() 的最小面积;若不存在,请说明理由
的最小面积;若不存在,请说明理由
【答案】(1)60°;(2)![]() ;(3)存在,
;(3)存在,![]()
【解析】
(1)由旋转可得:AC=A'C=2,进而得到BC=![]() ,依据∠A'BC=90°,可得cos∠A'CB=
,依据∠A'BC=90°,可得cos∠A'CB=![]() ,即可得到∠A'CB=30°,∠ACA'=60°;
,即可得到∠A'CB=30°,∠ACA'=60°;
(2)根据M为A'B'的中点,即可得出∠A=∠A'CM,进而得到PB= ![]() ,依据tan∠BQC=tan∠A=
,依据tan∠BQC=tan∠A=![]() ,即可得到BQ=BC×
,即可得到BQ=BC×![]() =2,进而得出PQ=PB+BQ=
=2,进而得出PQ=PB+BQ=![]() ;
;
(3)依据S四边形PA'B′Q=S△PCQ-S△A'CB'=S△PCQ-![]() ,即可得到S四边形PA'B′Q最小,即S△PCQ最小,而S△PCQ=
,即可得到S四边形PA'B′Q最小,即S△PCQ最小,而S△PCQ=![]() PQ×BC=
PQ×BC=![]() PQ,利用几何法或代数法即可得到S△PCQ的最小值=3,S四边形PA'B′Q=3-
PQ,利用几何法或代数法即可得到S△PCQ的最小值=3,S四边形PA'B′Q=3-![]() .
.
解(1)由旋转得:![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)因为M是![]() 中点,所以
中点,所以![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
∵∠PCQ=∠PBC=90°,
∴∠BQC+∠BPC=∠BCP+∠BPC=90°,
∴∠BQC=∠BCP=∠A,
![]() ,
,
![]() ,
,
![]() ;
;
(3) ![]() ,
,
![]() 最小,即
最小,即![]() 最小,
最小,
![]() ,
,
取PQ的中点G,
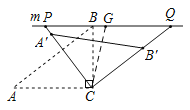
![]() ,即PQ=2CG,
,即PQ=2CG,
当![]() 最小时,
最小时, ![]() 最小,
最小,
![]() ,
, ![]() 与
与![]() 重合,
重合,![]() 最小,
最小,
∵![]() 的最小值为
的最小值为![]() ,
,![]()
![]() .
.

练习册系列答案
相关题目